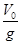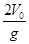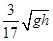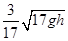题目内容
在某次自由式滑雪比赛中，一运动员从弧形雪坡上沿水平方向飞出后，又落回到斜面雪坡上，如图所示，若斜面雪坡的倾角为θ，飞出时的速度大小为v0，不计空气阻力，运动员飞出后在空中的姿势保持不变，重力加速度为g，则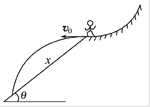
A．运动员在空中经历的时间是 |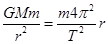
B．运动员落到雪坡时的速度大小是 |
| C．如果v0不同，则该运动员落到雪坡时的速度方向也就不同 |
| D．不论v0多大，该运动员落到雪坡时的速度方向都是相同的 |
D
解析试题分析：根据平抛运动的特点有，水平位移：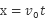
竖直位移：
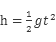
所以经历的时间：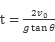
，竖直方向的速度：
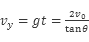，所以运动员落到雪坡时的速度大小是：
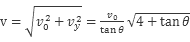所以AB错；设运动员落到雪坡时的速度方向与水平面的夹角
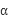，则有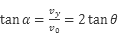
，所以D正确。考点： 平抛运动
练习册系列答案
相关题目
质量为m的小球做平抛运动，已知重力加速度为g，根据下列哪个条件可求出小球初速度
| A．水平位移 | B．下落高度 | C．落地时的动能 | D．落地时的速度大小和方向 |
物体在平抛运动的过程中，在相等的时间内，下列物理量相等的是( )
| A．速度的增量 | B．位移的增量 |
| C．位移 | D．平均速度 |
如图所示，放置在竖直平面内的光滑杆AB，是按照从高度为h处以初速度v0平抛的运动轨迹制成的，A端为抛出点，B端为落地点，现将一小球套于其上，由静止开始从轨道A端滑下，已知重力加速度为g，当小球到达轨道B端时( )
A．小球的速率为 |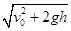
B．小球的速率为 |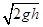
| C．小球在水平方向的速度大小为v0 |
D．小球在水平方向的速度大小为 |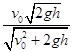
如图所示，在竖直面内有一个圆轨道，圆心为O。P为轨道上与O等高的最右端位置，一小球以某一初速度从p点水平向左抛出，落在圆轨道上的某一点，忽略一切阻力和能量损耗，则下列说法正确的是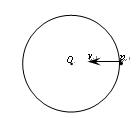
| A．小球初速度合适，可能垂直撞在圆轨道上 |
| B．小球初速度合适，位移大小等于直径 |
| C．初速度越大，落到圆轨道上的时间越长 |
| D．小球初速度合适，落在O点正下方的圆周上时间最长 |
如图所示，在同一平台上的O点水平抛出的三个物体，分别落到a、b、c三点，则三个物体运动的初速度va、vb、vc的关系和三个物体运动的时间ta、tb、tc的关系分别是（ ）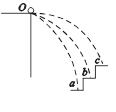
| A．va＞vb＞vcta＞tb＞tc |
| B．va＜vb＜vc ta＞tb＞tc |
| C．va＜vb＜vcta=tb=tc |
| D．va＞vb＞vcta＜tb＜tc |