题目内容
理论研究表明,物体在地球附近都受到地球对它的万有引力作用,具有引力势能.选物体在距地球无限远处的引力势能为零,则引力势能可表示为Ep=-
(其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离).现有一质量m′的人造卫星绕地球做圆周运动周期T.若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
| GMm | r |
分析:根据万有引力等于向心力求出人造卫星的轨道半径,从而得出在轨道上的动能和势能之和,根据能量守恒定律求出至少做功的多少.
解答:解:设卫星绕地球做圆周运动半径r′,牛顿第二定律得:
=m′r′
=m′
解得r′=
,EK=
mv2=
,在r′轨道上运动具有的机械能为E=EK+EP=
地面发射须做功W=△E=
-
.
答:若要从地面上将这颗卫星发射成功,则至少需做功为
-
.
| GMm′ |
| r′2 |
| 4π2 |
| T2 |
| v2 |
| r′ |
解得r′=
| 3 |
| ||
| 1 |
| 2 |
| GMm′ |
| 2r′ |
| -GMm′ |
| 2r′ |
地面发射须做功W=△E=
| GMm/ |
| R |
| GMm/ | |||||
2
|
答:若要从地面上将这颗卫星发射成功,则至少需做功为
| GMm/ |
| R |
| GMm/ | |||||
2
|
点评:解决本题的关键掌握万有引力提供向心力这一理论,以及知道至少做功的多少等于机械能的增量.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
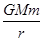 (其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
(其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)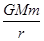 (其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/ 的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)
(其中G为万有引力常量,M为地球质量,m为物体的质量,r是物体到地心的距离)。现有一质量m/ 的人造卫星绕地球做圆周运动周期T。若要从地面上将这颗卫星发射成功,则至少需做多少功?(已知地球质量为M,半径为R,万有引力常量为G,且忽略空气阻力对卫星发射的影响)