题目内容
1957年第一颗人造卫星上天,开辟了人类宇航的新时代.四十多年来,人类不仅发射了人造地球卫星,还向宇宙空间发射了多个空间探测器.空间探测器要飞向火星等其它行星,甚至飞出太阳系,首先要克服地球对它的引力的作用.
理论研究表明,物体在地球附近都受到地球对它的万有引力的作用,具有引力势能,设物体在距地球无限远处的引力势能为零,则引力势能可以表示为E=-G=
,其中G是万有引力常量,M是地球的质量,m是物体的质量,r是物体距地心的距离.
现有一个空间探测器随空间站一起绕地球做圆周运动,运行周期为T,已知探测器的质量为m,地球半径为R,地面附近的重力加速度为g.要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它作多少功?
理论研究表明,物体在地球附近都受到地球对它的万有引力的作用,具有引力势能,设物体在距地球无限远处的引力势能为零,则引力势能可以表示为E=-G=
| Mm | r |
现有一个空间探测器随空间站一起绕地球做圆周运动,运行周期为T,已知探测器的质量为m,地球半径为R,地面附近的重力加速度为g.要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它作多少功?
分析:空间探测器随空间站一起绕地球做圆周运动,由地球的万有引力充当向心力,根据牛顿第二定律列式可求出空间站的轨道半径和速度,即可得到空间探测器具有的机械能.空间站要脱离地球的引力,机械能最小值为E∞=0,根据功能关系求功.
解答:解:空间探测器绕地球作圆周运动,有
由G
=m
r=m
得,空间站的轨道半径r=
随空间站一起运动时,空间探测器的动能为
mv2=
=
.
随空间站一起运动时,空间探测器具有的机械能为
E1=-G
+
mv2=-
空间站要脱离地球的引力,机械能最小值为E∞=0,因此,对探测器做功为
W=E∞-E1=
由地面附近的重力加速度g=G
得W=
答:要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它作
的功.
由G
| Mm |
| r2 |
| 4π2 |
| T2 |
| v2 |
| r |
| 3 |
| ||
随空间站一起运动时,空间探测器的动能为
| 1 |
| 2 |
| GMm |
| 2r |
| m |
| 2 |
| 3 | (
| ||
随空间站一起运动时,空间探测器具有的机械能为
E1=-G
| Mm |
| r |
| 1 |
| 2 |
| GMm |
| 2r |
空间站要脱离地球的引力,机械能最小值为E∞=0,因此,对探测器做功为
W=E∞-E1=
| GMm |
| 2r |
由地面附近的重力加速度g=G
| M |
| R2 |
| m |
| 2 |
| 3 | (
| ||
答:要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它作
| m |
| 2 |
| 3 | (
| ||
点评:对于卫星类型,要根据其运动模型,由万有引力定律、圆周运动规律和功能关系求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
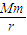 ,其中G是万有引力常量,M是地球的质量,m是物体的质量,r是物体距地心的距离.
,其中G是万有引力常量,M是地球的质量,m是物体的质量,r是物体距地心的距离.