题目内容
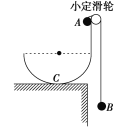
【题目】固定在竖直平面内的半圆形轨道与竖直轨道平滑连接,竖直轨道的上端有一个大小可忽略的小定滑轮,半圆形轨道的半径为R,C为轨道的最低点,竖直轨道高也为R,两个质量分别为2m和m的小球A和B用轻质细线连在一起,所有接触面均光滑,如图所示.开始时用手固定B、使A紧靠近滑轮,突然撤去手后,A由静止开始下滑,求A经过C点时的速度.
【答案】![]()
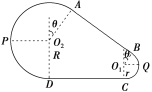
【解析】对A、B,从A静止释放到运动至C点,设A运动至C点时A、B的速度分别为v1、v2(关系如图所示).
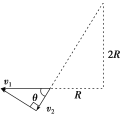
由几何关系知小滑轮到C的距离为s=![]() R
R
cos θ=![]()
因为细线长度不变,则B上升的高度H=s
在A下滑到C点的过程中,A、B系统机械能守恒,有
(2m)g(2R)-mgH=![]() (2m)v+
(2m)v+![]() mv
mv
B的速度大小等于A的速度沿细线方向的分速度大小,有v2=v1cos θ
联立以上各式解得v1=![]() .
.

练习册系列答案
相关题目