题目内容
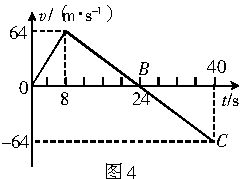
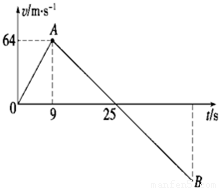
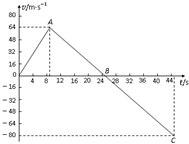 一行星探测器从所探测的行星表面垂直升空,假设探测器质量m恒为1500kg,发动机推力为恒力,探测器升空途中某时刻发动机突然关闭.如图是探测器的速度随时间变化的全过程图示.假设行星表面没有空气,问:
一行星探测器从所探测的行星表面垂直升空,假设探测器质量m恒为1500kg,发动机推力为恒力,探测器升空途中某时刻发动机突然关闭.如图是探测器的速度随时间变化的全过程图示.假设行星表面没有空气,问:(1)升空后9s、25s、45s(即图中A、B、C三点),探测器的运动情况如何?
(2)探测器在行星表面达到的最大高度?
(3)计算发动机的推力.
分析:(1)探测器先加速上升,然后减速上升,最后加速下降;根据图线计算分析讨论;
(2)图象在0-25范围内“面积”表示探测器在行星表面达到的最大高度,由数学知识求解.
(3)发动机关闭后,探测器的加速度等于该行星表面的重力加速度,由图象的斜率求出.在0-9s时间内,由斜率求出加速度,根据牛顿第二定律求出发动机的推动力.
(2)图象在0-25范围内“面积”表示探测器在行星表面达到的最大高度,由数学知识求解.
(3)发动机关闭后,探测器的加速度等于该行星表面的重力加速度,由图象的斜率求出.在0-9s时间内,由斜率求出加速度,根据牛顿第二定律求出发动机的推动力.
解答:解:(1)A点为发动机关闭时的对应点,此时探测器将以64 m/s作竖直上抛运动;B点速度为零,到达了最高点;从出发点到C点的总位移为:
x=
×64×25-
×(45-25)×80=0,所以C点表示落地点
(2)B点速度为零,到达了最高点,则s=
×25×64=800m
(3)根据图象得:匀加速运动时a=
=
=7.1m/s2
匀减速运动时a′=
=
=4m/s2
根据牛顿第二定律得:F-ma′=ma
解得:F-m(a+a′)=16700N
答:(1)A点为发动机关闭时的对应点,此时探测器将以64 m/s作竖直上抛运动;B点到达了最高点;C点表示落地点;
(2)探测器在行星表面达到的最大高度为800m;
(3)计算发动机的推力为16700N.
x=
| 1 |
| 2 |
| 1 |
| 2 |
(2)B点速度为零,到达了最高点,则s=
| 1 |
| 2 |
(3)根据图象得:匀加速运动时a=
| △v |
| △t |
| 64 |
| 9 |
匀减速运动时a′=
| △v′ |
| △t′ |
| 64 |
| 25-9 |
根据牛顿第二定律得:F-ma′=ma
解得:F-m(a+a′)=16700N
答:(1)A点为发动机关闭时的对应点,此时探测器将以64 m/s作竖直上抛运动;B点到达了最高点;C点表示落地点;
(2)探测器在行星表面达到的最大高度为800m;
(3)计算发动机的推力为16700N.
点评:本题关键分析清楚探测器的运动规律,然后根据运动学公式结合牛顿第二定律列式求解.

练习册系列答案
相关题目

(1)探测器在行星表面达到的最大高度是______ m;
(2)该行星表面的重力加速度是________m/s2;
(3)计算发动机的推动力是________N。
(2)该行星表面的重力加速度是________m/s2;
(3)计算发动机的推动力是________N。
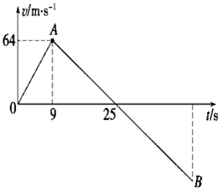 一行星探测器从所探测的行星表面垂直升空.假设探测器的质量为1500kg,发动机推力为恒力,探测器升空途中某时刻发动机突然关闭.如图所示是探测器的速度随时间变化的全过程图示.假设行星表面没有空气.则:
一行星探测器从所探测的行星表面垂直升空.假设探测器的质量为1500kg,发动机推力为恒力,探测器升空途中某时刻发动机突然关闭.如图所示是探测器的速度随时间变化的全过程图示.假设行星表面没有空气.则: