题目内容
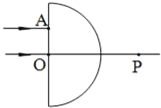
【题目】如图所示，在半径为R的圆形区域内充满磁感应强度为B的匀强磁场，MN是一竖直放置的感光板．从圆形磁场最高点P以速度v垂直磁场正对着圆心O射入带正电的粒子，且粒子所带电荷量为q、质量为m,不考虑粒子重力，关于粒子的运动，以下说法正确的是( )
A. 粒子在磁场中通过的弧长越长时间也越长
B. 出磁场的粒子其出射方向的反向延长线也一定过圆心0
C. 只要速度满足v＝
，入射的粒子出射后一定垂直打在MN上
D. 出磁场的粒子一定能垂直打在MN上
【答案】BC
【解析】试题分析：带电粒子射入磁场后做匀速圆周运动，对着圆心入射，必将沿半径离开圆心，根据洛伦兹力充当向心力，求出
时轨迹半径，确定出速度的偏向角．对着圆心入射的粒子，速度越大在磁场中通过的弧长越长，轨迹对应的圆心角越小，即可分析时间关系．
根据周期公式
可知粒子在磁场中的运动周期和速度无关，即所有粒子在磁场中的运动周期相同，粒子在
，即粒子在磁场中的运动轨迹的圆心角越大，运动时间越大，对着圆心入射的粒子，速度越大在磁场中通过的弧长越长，轨迹对应的圆心角越小，即运动时间越小，A错误；带电粒子的运动轨迹是圆弧，根据几何知识可知，对着圆心入射的粒子，其出射方向的反向延长线也一定过圆心，B正确；速度满足
时，粒子的轨迹半径为
，入射点、出射点、O点与轨迹的圆心构成菱形，射出磁场时的轨迹半径与最高点的磁场半径平行，粒子的速度一定垂直打在MN板上，故C正确D错误．
练习册系列答案
相关题目
