题目内容
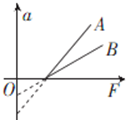
物体A、B都静止在同一水平面上,它们的质量分别为mA、mB,与水平面间的动摩擦因数分别为μA、μB,用水平拉力F拉物体A、B,所得加速度a与拉力F关系图线如图中A、B所示,则有( )
| A.μA=μB,mA>mB | B.μA>μB,mA<mB |
| C.可能有mA=mB | D.μA<μB,mA>mB |

对质量为m的物体受力分析,假定动摩擦因素为μ,根据牛顿第二定律,有
F-μmg=ma
解得:
a=
F-μg,
故a与F关系图象的斜率表示质量的倒数,故mA<mB;
从图象可以看出纵轴截距用表示-μg表示,故μA>μB;
故选B.
F-μmg=ma
解得:
a=
| 1 |
| m |
故a与F关系图象的斜率表示质量的倒数,故mA<mB;
从图象可以看出纵轴截距用表示-μg表示,故μA>μB;
故选B.

练习册系列答案
相关题目
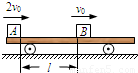
 如图所示,A、B两物体重力都等于10N,各接触面间的动摩擦因数都等于0.3,同时有F=2N的两个水平力分别作用在A和B上,A和B均静止,则地面对B和B对A的摩擦力分别为( )
如图所示,A、B两物体重力都等于10N,各接触面间的动摩擦因数都等于0.3,同时有F=2N的两个水平力分别作用在A和B上,A和B均静止,则地面对B和B对A的摩擦力分别为( )| A、6N,3N | B、1N,1N | C、0,3N | D、0,2N |
 如图所示,A、B两物体重力都等于10N,各接触面间的动摩擦因数都等于0.3,同时有F=1N的两个水平力分别作用在A和B上,A和B均静止,则地面对B和B对A的摩擦力分别为( )
如图所示,A、B两物体重力都等于10N,各接触面间的动摩擦因数都等于0.3,同时有F=1N的两个水平力分别作用在A和B上,A和B均静止,则地面对B和B对A的摩擦力分别为( )| A、6 N;3N | B、1 N;1 N | C、0;1 N | D、0;2 N |
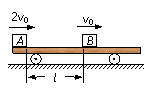
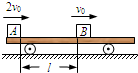 如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求:
如图所示,一平板小车静止在光滑水平面上,质量均为m的物体A、B分别以2v0和v0的初速度,沿同一直线同时同向水平滑上小车,刚开始滑上小车的瞬间,A位于小车的最左边,B位于距小车左边l处.设两物体与小车间的动摩擦因数均为μ,小车的质量也为m,最终物体A、B都停在小车上.求: