题目内容
14.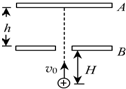 如图所示,水平放置的A、B两平行板相距h,有一个质量为m,带电量为+q的小球在B板之下H处以初速度v0竖直向上进入两板间;忽略重力作用,欲使小球恰好打到A板,试讨论A、B板间的电势差是多大?
如图所示,水平放置的A、B两平行板相距h,有一个质量为m,带电量为+q的小球在B板之下H处以初速度v0竖直向上进入两板间;忽略重力作用,欲使小球恰好打到A板,试讨论A、B板间的电势差是多大?
分析 如图,平行板电容器上极板A带正电,下极板B带负电,电场方向向下.质量为m,带电量为+q的小球从B板进入电场后受到重力和电场力,电场力方向向下,对小球做负功,小球刚好打到A板时,速度恰好为零,电场力做功为qUBA=-qUAB,整个过程中重力做功为-mg(H+h).根据动能定理求解电势差UAB
解答 解:当电场力方向向下时,UA>UB,电场力做负功,由动能定理得:
-qUAB-mg(H+h)=-$\frac{1}{2}$$m{v}_{0}^{2}$
解得:UAB=m$\frac{{v}_{0}^{2}-2g(H+h)}{2q}$
当电场力方向向上时,UA<UB,电场力做正功,由动能定理得:
qUBA-mg(H+h)=-$\frac{1}{2}$$m{v}_{0}^{2}$
解得:UBA=m$\frac{2g(H+h)-{v}_{0}^{2}}{2q}$
答:A、B板间的电势差是m$\frac{{v}_{0}^{2}-2g(H+h)}{2q}$ 或m$\frac{2g(H+h)-{v}_{0}^{2}}{2q}$.
点评 本题涉及两个过程,采用全程法运用动能定理研究,比较简洁,也可以分段研究,运用牛顿第二定律和运动学公式结合研究

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
2. 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合电键S,将滑动变阻器的滑动触头P从最左端滑到最右端的过程中,电压表(内阻极大)的示数与电流表示数的关系图线如图(b)所示.则( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合电键S,将滑动变阻器的滑动触头P从最左端滑到最右端的过程中,电压表(内阻极大)的示数与电流表示数的关系图线如图(b)所示.则( )
 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合电键S,将滑动变阻器的滑动触头P从最左端滑到最右端的过程中,电压表(内阻极大)的示数与电流表示数的关系图线如图(b)所示.则( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合电键S,将滑动变阻器的滑动触头P从最左端滑到最右端的过程中,电压表(内阻极大)的示数与电流表示数的关系图线如图(b)所示.则( )| A. | 电源电动势为4伏 | B. | 电源内电阻的阻值为10Ω | ||
| C. | 定值电阻R1阻值为10Ω | D. | 滑动变阻器R2的最大阻值为20Ω |
9.下列说法正确的是( )
| A. | 变速直线运动的速度是变化的 | |
| B. | 平均速度即为速度的平均值 | |
| C. | 瞬时速度是物体在某一时刻或在某一位置时的速度 | |
| D. | 平均速度粗略描述物体在某段时间内运动的快慢 |
19.关于电场线的下列说法中正确的是( )
| A. | 电场线上每点的切线方向都跟该点的场强方向一致 | |
| B. | 电场线就是电荷在电场中的轨迹线 | |
| C. | 在电场中有电场线的地方场强有可能为零 | |
| D. | 点电荷电场在同一平面内的电场线是以点电荷为中心的一簇同心圆 |

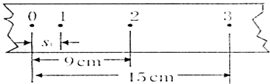 某同学做了一次较为精确的测定匀加速直线运动的加速度的实验,实验所得到的纸带如图所示.设0点是计数的起始点,两计数点之间的时间间隔为0.1s.则第一个计数点与0点的距离s1应为4cm,物体的加速度a=1m/s2.如果当时电网中交变电流的频率是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比偏小(选填:偏大、偏小或不变).
某同学做了一次较为精确的测定匀加速直线运动的加速度的实验,实验所得到的纸带如图所示.设0点是计数的起始点,两计数点之间的时间间隔为0.1s.则第一个计数点与0点的距离s1应为4cm,物体的加速度a=1m/s2.如果当时电网中交变电流的频率是f=51Hz,而做实验的同学并不知道,那么加速度的测量值与实际值相比偏小(选填:偏大、偏小或不变). 一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,已知波的传播速度v=2m/s.
一列沿x轴正方向传播的简谐横波在t=0时刻的波形如图所示,已知波的传播速度v=2m/s.