题目内容
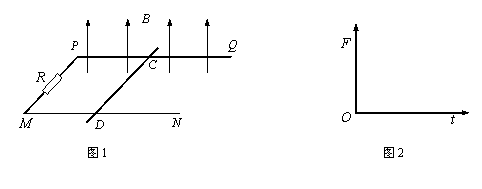
如图1所示,两根间距为l1的平行导轨PQ和MN处于同一水平面内,左端连接一阻值为R的电阻,导轨平面处于竖直向上的匀强磁场中.一质量为m、横截面为正方形的导体棒CD垂直于导轨放置,棒到导轨左端PM的距离为l2,导体棒与导轨接触良好,不计导轨和导体棒的电阻.
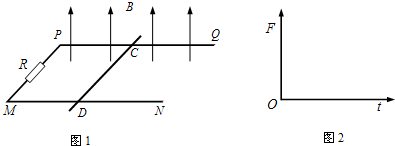
(1)若CD棒固定,已知磁感应强度B的变化率
随时间t的变化关系式为
=ksinωt,求回路中感应电流的有效值I;
(2)若CD棒不固定,棒与导轨间最大静摩擦力为fm,磁感应强度B随时间t变
化的关系式为B=kt.求从t=0到CD棒刚要运动,电阻R上产生的焦耳热Q;
(3)若CD棒不固定,不计CD棒与导轨间的摩擦;磁场不随时间变化,磁感应强度为B.现对CD棒施加水平向右的外力F,使CD棒由静止开始向右以加速度a做匀加速直线运动.请在图2中定性画出外力F随时间t变化的图象,并求经过时间t0,外力F的冲量大小I.
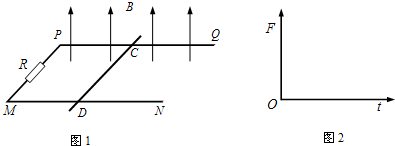
(1)若CD棒固定,已知磁感应强度B的变化率
| △B |
| △t |
| △B |
| △t |
(2)若CD棒不固定,棒与导轨间最大静摩擦力为fm,磁感应强度B随时间t变
化的关系式为B=kt.求从t=0到CD棒刚要运动,电阻R上产生的焦耳热Q;
(3)若CD棒不固定,不计CD棒与导轨间的摩擦;磁场不随时间变化,磁感应强度为B.现对CD棒施加水平向右的外力F,使CD棒由静止开始向右以加速度a做匀加速直线运动.请在图2中定性画出外力F随时间t变化的图象,并求经过时间t0,外力F的冲量大小I.
(1)根据法拉第电磁感应定律
回路中的感应电动势e=
=kl1l2sinωt
所以,电动势的最大值 Em=kl1l2
由闭合电路欧姆定律 Im=
=
由于交变电流是正弦式的,所以感应电流的有效值I=
Im
解得,I=
(2)根据法拉第电磁感应定律,回路中的感应电动势 E=l1l2
=kl1l2
根据闭合电路欧姆定律 I=
=
CD杆受到的安培力 FA=BIl1=
t
当CD杆将要开始运动时,满足:FA=fm
由上式解得:CD棒运动之前,产生电流的时间t=
所以,在时间t内回路中产生的焦耳热Q=I2Rt=fml2
(3)CD棒切割磁感线产生的感应电动势E=Bl1v
时刻t的感应电流I=
=
CD棒在加速过程中,根据由牛顿第二定律 F-BIl1=ma
解得:F=
t+ma
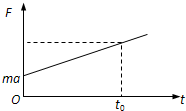
根据上式,可得到外力F随时间变化的图象如图所示,由图象面积可知:经过时间t0,外力F的冲量I
I=
[(
t0+ma)+ma]t0
解得:I=
+mat0
答:
(1)回路中感应电流的有效值I为
;
(2)从t=0到CD棒刚要运动,电阻R上产生的焦耳热Q为fml2;
(3)在图2中定性画出外力F随时间t变化的图象如图所示,经过时间t0,外力F的冲量大小I为
+mat0.
回路中的感应电动势e=
| △Φ |
| △t |
所以,电动势的最大值 Em=kl1l2
由闭合电路欧姆定律 Im=
| Em |
| R |
| kl1l2 |
| R |
由于交变电流是正弦式的,所以感应电流的有效值I=
| ||
| 2 |
解得,I=
| kl1l2 | ||
|
(2)根据法拉第电磁感应定律,回路中的感应电动势 E=l1l2
| △B |
| △t |
根据闭合电路欧姆定律 I=
| E |
| R |
| kl1l2 |
| R |
CD杆受到的安培力 FA=BIl1=
k2
| ||
| R |
当CD杆将要开始运动时,满足:FA=fm
由上式解得:CD棒运动之前,产生电流的时间t=
| fmR | ||
k2
|
所以,在时间t内回路中产生的焦耳热Q=I2Rt=fml2
(3)CD棒切割磁感线产生的感应电动势E=Bl1v
时刻t的感应电流I=
| E |
| R |
| Bl1at |
| R |
CD棒在加速过程中,根据由牛顿第二定律 F-BIl1=ma
解得:F=
B2
| ||
| R |
根据上式,可得到外力F随时间变化的图象如图所示,由图象面积可知:经过时间t0,外力F的冲量I
I=
| 1 |
| 2 |
B2
| ||
| R |
解得:I=
B2
| ||||
| 2R |

答:
(1)回路中感应电流的有效值I为
| kl1l2 | ||
|
(2)从t=0到CD棒刚要运动,电阻R上产生的焦耳热Q为fml2;
(3)在图2中定性画出外力F随时间t变化的图象如图所示,经过时间t0,外力F的冲量大小I为
B2
| ||||
| 2R |

练习册系列答案
相关题目
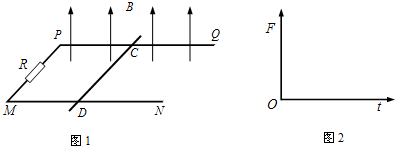

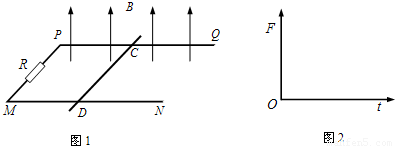
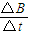 随时间t的变化关系式为
随时间t的变化关系式为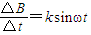 ,求回路中感应电流的有效值I;
,求回路中感应电流的有效值I;