��Ŀ����
����Ŀ����ͼ��ʾ��ij���ֳ���ɽ��������װ��ԭ��ͼ���⻬�Ļ��ι��ĩ����һ���뾶ΪR�Ĺ⻬Բ���ƽ�����ӣ�����(A�����£�B������)�������ֱ�ΪmA��4m��mB��m������Ϊ�ʵ㣩���м��סһ�ᵯ�ɺ�����һ�������ӹ⻬���ι���ϵ�ijһ�߶��ɾ�ֹ���£��������ջ���Բ����͵�ʱ���������Ĺҹ�ͻȻ�Ͽ������ɽ���������������B���պ�ͣ��Բ����͵㴦��A����Բ������˶�ǡ��Խ��Բ�������ߵ㣮���������ٶ�Ϊg����
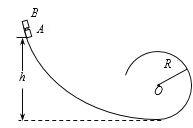
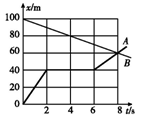
��1��A��������ʱ���ٶȣ�
��2����ǰ�����������е����ͷŵĵ������ܣ�
��3�������»��ĸ߶�h��
���𰸡���1��v1��![]() ����2�� EP��2mgR ����3�� h��
����2�� EP��2mgR ����3�� h��![]()
��������(1)��ǰ������ߵ��ٶ�Ϊv2���������У�![]()
��ǰ������͵�λ���������ٶ�Ϊv1�����ݻ�е���غ�ã�![]()
������ã�![]()
(2) ����������ǰ�ٶ�Ϊv0���ɶ����غ㶨��2mv0=mv1
��:![]()
�����ǰ���ɵ�������Ep������ϵͳ��е���غ��:![]()
(3) ������h�ߴ��˶�����ʹ���е���غ�![]()
![]()

��ϰ��ϵ�д�
 �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
�����Ŀ