题目内容
14. 如图所示,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r的$\frac{1}{4}$细圆管CD,管口D端正下方竖直光滑圆管内直立一根劲度系数为k的轻弹簧,轻弹簧一端固定,另一端恰好与管口D端齐平.质量为m的小球从曲面上A点由静止开始下滑,AB竖直高度为2r,BC的长度为3r,进入管口C端时与圆管恰好无作用力,通过CD后压缩弹簧(始终在弹性限度内).若当地重力加速度为g,求:
如图所示,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接内壁光滑、半径为r的$\frac{1}{4}$细圆管CD,管口D端正下方竖直光滑圆管内直立一根劲度系数为k的轻弹簧,轻弹簧一端固定,另一端恰好与管口D端齐平.质量为m的小球从曲面上A点由静止开始下滑,AB竖直高度为2r,BC的长度为3r,进入管口C端时与圆管恰好无作用力,通过CD后压缩弹簧(始终在弹性限度内).若当地重力加速度为g,求:(1)小球达到B点时的速度大小vB;
(2)BC段的动摩擦因数μ;
(3)通过计算说明小球最终停在何处.
分析 (1)A到B的过程中只有重力做功,根据机械能守恒定律或动能定理求出小球到达B点的速度大小.
(2)根据牛顿第二定律求出小球在C点时的速度.从A到B,根据动能定理求出BC段的动摩擦因数μ.
(3)由于BC段有摩擦,最终小球由于机械能不断减小而停止运动,对整个过程,运用能量守恒求出小球在BC上滑行的总路程,从而确定最终停止的位置.
解答 解:(1)从A到B,根据动能定理有:mg•2r=$\frac{1}{2}$mvB2
解得 vB=2$\sqrt{gr}$
(2)由于进入管口C端时与圆管恰好无作用力,即只由重力提供向心力
即 mg=m$\frac{{v}_{C}^{2}}{r}$
从B到C,由动能定理得:-μmg•3r=$\frac{1}{2}$mvC2-$\frac{1}{2}m{v}_{B}^{2}$
解得:μ=0.5
(3)根据能量守恒,从A点到最终有
mg•2r=μmgs
解得小球在BC上滑行的总路程 s=4r
因此小球最终停在C点左边r处(或B点右边2r处).
答:
(1)小球达到B点时的速度大小vB是2$\sqrt{gr}$.
(2)BC段的动摩擦因数μ是0.5;
(3)小球最终停在C点左边r处(或B点右边2r处).
点评 本题综合运用了机械能守恒定律、动能定理、功能关系以及牛顿第二定律,关键要灵活选择研究的过程,准确把握圆周运动的临界条件.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
4.下列说法正确的是( )
| A. | 做曲线运动的物体的合力可能是恒定的 | |
| B. | 不在同一直线上的两个匀速直线运动的合运动一定是直线运动 | |
| C. | 做匀速圆周运动的物体的加速度是不变的 | |
| D. | 若运动时间足够长,做平抛运动物体的速度方向最终为竖直方向 |
5.“神舟十号”飞船绕地球的运行可视为匀速圆周运动,其轨道高度距离地面约340km,则关于飞船的运行,下列说法中正确的是( )
| A. | 飞船处于平衡状态 | |
| B. | 地球对飞船的万有引力提供飞船运行的向心力 | |
| C. | 飞船运行的速度小于第一宇宙速度 | |
| D. | 飞船运行的加速度小于地球表面的重力加速度 |
2.物体做竖直上抛运动,在落回抛出点时该物体的速率是30m/s,那么物体(g取10m/s2)( )
| A. | 由抛出到落回抛出点的时间是3 s | |
| B. | 只有在2 s末时经过40 m高处 | |
| C. | 经过25 m高处时的瞬时速率只能是20 m/s | |
| D. | 上升的最大高度是90 m |
9. 如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )
如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )
 如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )
如图所示,长为l的轻杆末端固定一个小球,在竖直平面内做圆周运动,当地重加速度为g,则当小球运动到最高点时( )| A. | 向心力一定只由重力提供 | |
| B. | 受到杆的弹力不可能为零 | |
| C. | 若速率为$\sqrt{gl}$,则轻杆对小球有向上的支持力 | |
| D. | 若速率为$\sqrt{2gl}$,则轻杆对小球有向下的拉力 |
19.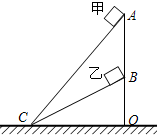 如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.则( )
如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.则( )
 如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.则( )
如图所示,A、C和B、C是两个固定的斜面,斜面的顶端A、B在同一竖直线上.甲、乙两个小物体在同一竖直线上.甲、乙两个小物块分别从斜面AC和BC顶端由静止开始下滑,质量分别是m1、m2(m1<m2),与斜面间的动摩擦因数均为μ.若甲、乙滑至底端C的过程中克服摩擦力做的功分别是W1、W2,所需时间分别是t1、t2.则( )| A. | EK1>EK2 | B. | v1>v2 | C. | W1<W2 | D. | t1<t2 |
3. 如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g.则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g.则小滑块( )
 如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g.则小滑块( )
如图所示,在竖直平面内有一固定轨道,其中AB是长为R的粗糙水平直轨道,BCD是圆心为O、半径为R的$\frac{3}{4}$光滑圆弧轨道,两轨道相切于B点,在推力作用下,质量为m的小滑块从A点由静止开始做匀加速直线运动,到达B点时即撤去推力,小滑块恰好能沿圆轨道经过最高点C重力加速度大小为g.则小滑块( )| A. | 在AB段运动的加速度为2.5g | |
| B. | 到C点时速度为零 | |
| C. | 沿圆轨道上滑时动能与重力势能相等的位置在OD上方 | |
| D. | 在C点时合外力的瞬时功率为mg$\sqrt{gR}$ |