题目内容
【题目】车站、码头、机场等使用的货物安检装置的示意图如图所示，绷紧的传送带始终保持υ=1m/s的恒定速率运行，AB为水平传送带部分且足够长，现有一质量为m=5kg的行李包（可视为质点）无初速度的放在水平传送带的A端，传送到B端时没有被及时取下，行李包从B端沿倾角为37°的斜面滑入储物槽，已知行李包与传送带的动摩擦因数为0.5，行李包与斜面间的动摩擦因数为0.8，g=10m/s2 ， 不计空气阻力（sin37°=0.6，cos37°=0.8）．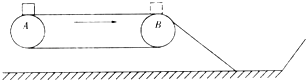
（1）行李包相对于传送带滑动的距离．
（2）若B轮的半径为R=0.2m，求行李包在B点对传送带的压力；
（3）若行李包滑到储物槽时的速度刚好为零，求斜面的长度．
【答案】
（1）
解：行李包在水平传送带上有摩擦力产生加速度，由牛顿第二定律得：
μ1mg=ma1
所以： 
行李包到达传送带的速度需要的时间：v=a1t1
所以： 
s
行李包前进的距离： 
传送带前进的距离：x2=vt1
行李包相对于传送带的距离：△x=x2﹣x1
代入数据解得：△x=0
（2）
解：行李包在B点受到重力和支持力的作用，由牛顿第二定律可知：
mg﹣F= 
代入数据得：F=25N
根据牛顿第三定律，行李包在B点对传送带的压力大小是25N，方向竖直向下
（3）
解：行李包在斜面上受到重力、支持力和摩擦力的作用，沿斜面向下的方向：
μ2mgcos37°﹣mgsin37°=ma2
要使它到达底部时的速度恰好为0，则：0﹣v2=﹣2a2x
代入数据解得：x=1.25m
【解析】（1）水平方向行李包受到摩擦力的作用做匀加速直线运动，由牛顿第二定律求出加速度，由v=at求出运动的时间，根据时间和加速度求出水平距离以及二者水平位移的差．（2）行李包在B点受到重力和支持力的作用，由牛顿第二定律即可求得支持力；压力大小等于支持力；（3）根据受力分析，结合牛顿第二定律求出行李包在斜面上的加速度，然后结合题目的条件即可求出．
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值．
