题目内容
16. 如图为儿童娱乐的滑梯示意图,其中AB为长s1=3.0m的斜面滑槽,与水平方向夹角为θ=37°,BC为水平滑槽,AB与BC连接处通过一段短圆弧相连,BC右端与半径R=0.20m的$\frac{1}{4}$圆弧CD相切,ED为地面.儿童在娱乐时从A处由静止下滑,设该儿童与斜面滑槽及与水平滑槽间的动摩擦因数均为μ=0.50.(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
如图为儿童娱乐的滑梯示意图,其中AB为长s1=3.0m的斜面滑槽,与水平方向夹角为θ=37°,BC为水平滑槽,AB与BC连接处通过一段短圆弧相连,BC右端与半径R=0.20m的$\frac{1}{4}$圆弧CD相切,ED为地面.儿童在娱乐时从A处由静止下滑,设该儿童与斜面滑槽及与水平滑槽间的动摩擦因数均为μ=0.50.(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:(1)该儿童滑到斜面底端B点时的速度大小vB.
(2)为使该儿童滑下后不会从C处平抛出去,滑至C时速度vC不应超过多大?水平滑槽BC长度s2至少应为多少?(以上结果均保留二位有效数字)
分析 (1)根据牛顿第二定律求出儿童下滑的加速度,结合速度位移公式求出B点的速度.
(2)根据牛顿第二定律求出C点的最大速度,结合动能定理求出BC长度的最小值.
解答 解:(1)儿童从A滑到B,由牛顿第二定律得,mgsin37°-μmgcos37°=ma,
由运动学公式得,${{v}_{B}}^{2}=2a{s}_{1}$,
代入数据解得vB=3.5m/s.
(2)当儿童恰好从C处平抛,则在C处不受弹力作用,
$mg=m\frac{{{v}_{C}}^{2}}{R}$,
代入数据解得vC=1.4m/s.
儿童从B到C处,由动能定理得,$-μmg{s}_{2}=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{B}}^{2}$,
代入数据解得s2=1.0m.
要使儿童不从C处平抛出去,水平滑道BC长度 应大于1.0m.
答:(1)儿童滑到斜面底端B点时的速度大小为3.5m/s;
(2)滑至C时速度vC不应超过1.4m/s,水平滑槽BC长度s2至少应为1.0m.
点评 本题考查了牛顿第二定律、动能定理和运动学公式的综合运用,知道C点做平抛运动的临界条件是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.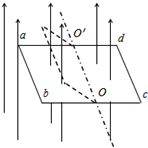 如图所示,匀强磁场的磁感应强度方向设置向上,大小为B,用电阻率为ρ、横截面积为S外表绝缘的导线做成边长为l的正方形线圈abcd水平放置,O、O′为过ad、bc两边中点的直线,线框全部位于磁场中,现将线框右半部分固定不动,而把线框左半部分以OO′为轴,以角速度ω绕OO′顺时针匀速转动180°,设此过程中通过导线横截面的电荷量为q,整个线框中产生的焦耳热为Q,则下列说法正确的是( )
如图所示,匀强磁场的磁感应强度方向设置向上,大小为B,用电阻率为ρ、横截面积为S外表绝缘的导线做成边长为l的正方形线圈abcd水平放置,O、O′为过ad、bc两边中点的直线,线框全部位于磁场中,现将线框右半部分固定不动,而把线框左半部分以OO′为轴,以角速度ω绕OO′顺时针匀速转动180°,设此过程中通过导线横截面的电荷量为q,整个线框中产生的焦耳热为Q,则下列说法正确的是( )
 如图所示,匀强磁场的磁感应强度方向设置向上,大小为B,用电阻率为ρ、横截面积为S外表绝缘的导线做成边长为l的正方形线圈abcd水平放置,O、O′为过ad、bc两边中点的直线,线框全部位于磁场中,现将线框右半部分固定不动,而把线框左半部分以OO′为轴,以角速度ω绕OO′顺时针匀速转动180°,设此过程中通过导线横截面的电荷量为q,整个线框中产生的焦耳热为Q,则下列说法正确的是( )
如图所示,匀强磁场的磁感应强度方向设置向上,大小为B,用电阻率为ρ、横截面积为S外表绝缘的导线做成边长为l的正方形线圈abcd水平放置,O、O′为过ad、bc两边中点的直线,线框全部位于磁场中,现将线框右半部分固定不动,而把线框左半部分以OO′为轴,以角速度ω绕OO′顺时针匀速转动180°,设此过程中通过导线横截面的电荷量为q,整个线框中产生的焦耳热为Q,则下列说法正确的是( )| A. | q=$\frac{BSI}{4ρ}$,Q=$\frac{π{B}^{2}ω{l}^{3}S}{32ρ}$ | B. | q=$\frac{BSl}{8ρ}$,Q=$\frac{π{B}^{2}ω{l}^{3}S}{16ρ}$ | ||
| C. | q=$\frac{BSl}{4ρ}$,Q=$\frac{{B}^{2}ω{l}^{3}S}{4πρ}$ | D. | q=0,Q=$\frac{π{B}^{2}ω{l}^{3}S}{32ρ}$ |
7.物理学发展到今天的程度,推动了人类文明的极大进步.以下对几位物理学家所作科学贡献,叙述正确的是( )
| A. | 牛顿在前人研究基础上总结出万有引力定律,并第一个测出引力常数为G | |
| B. | 汤姆生提出原子的核式结构学说,后来卢瑟福用α粒子散射实验给予验证 | |
| C. | 牛顿推翻了亚里士多德的“重的物体下落快”观点 | |
| D. | 奥斯特发现了电流的磁效应,法拉第发现了电磁感应现象 |
4.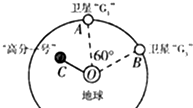 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
 2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
2014年3月8日凌晨马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”以及“高分一号”均可认为绕地心O做匀速圆周运动.卫星“G1”和“G3”的轨道半径为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置.若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )| A. | 卫星“G1”和“G3”的加速度大小相等均为$\frac{R}{r}$g | |
| B. | 如果调动“高分一号”卫星快速到达B位置的下方,必须对其减速 | |
| C. | “高分一号”是低轨道卫星,其所在高度有稀薄气体,运行一段时间后,高度会降低,速度增大,机械能会减小 | |
| D. | 卫星“”由位置A运动到位置B所需的时间为$\frac{2πr}{3R}$$\sqrt{\frac{r}{g}}$ |
11.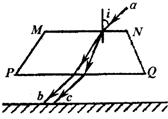 如图所示,一束较细的白光α以入射角i斜射到平行玻璃砖的MN界面后发生折射,再经PQ界面射出照到光屏上,则( )
如图所示,一束较细的白光α以入射角i斜射到平行玻璃砖的MN界面后发生折射,再经PQ界面射出照到光屏上,则( )
 如图所示,一束较细的白光α以入射角i斜射到平行玻璃砖的MN界面后发生折射,再经PQ界面射出照到光屏上,则( )
如图所示,一束较细的白光α以入射角i斜射到平行玻璃砖的MN界面后发生折射,再经PQ界面射出照到光屏上,则( )| A. | 逐渐增大入射角i,可使光射到PQ面时发生全反射 | |
| B. | 逐渐减小入射角i,可使光射到PQ面时发生全反射 | |
| C. | 色光b的光子能量一定小于色光c | |
| D. | 若玻璃砖界面MN和PQ不平行,则从PQ出射的各色光仍会相互平行 |
1.某同学参加跳水比赛.假如她质量为m,进入水中受到阻力而减速运动,假设水对她的阻力恒为F,那么她在水中下降高度为h的过程中,下列说法正确的是( )
| A. | 她的动能减少了Fh | B. | 她的重力势能减少了Fh | ||
| C. | 她的机械能减少了(F-mg)h | D. | 她的机械能减小了Fh |
8.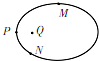 如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
 如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )
如图所示,带正电的点电荷固定在Q点,一电子仅在库仑力作用下,做以Q点为焦点的椭圆运动,M、P、N为椭圆上的三点,P点是轨道上离Q最近的点.vM、vN和EM、EN分别表示该电子在M、N两点的速度和电势能,则电子从M点逆时针运动到N点( )| A. | 电子的动能先减小后增大 | B. | 电场力对电子做了负功 | ||
| C. | vM<vN,EM>EN | D. | vM<vN,EM<EN |
5. 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
 如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )
如图所示,a、b、c、d是某匀强电场中的四个点,它们正好是一个矩形的四个顶点,且ab=cd=L,ad=bc=2L,电场线与矩形所在平面平行.已知a点电势为10V,b点电势为12V,d点电势为6V.一质子经过电场中的b点时速度为υ0,υ0方向与bc成45°角.一段时间后该质子经过电场中的c点.不计质子的重力.下列判断正确的是( )| A. | c点电势为8V | |
| B. | 场强大小为$\frac{4}{{\sqrt{2}L}}$ | |
| C. | 质子从b运动到c,所用的时间为$\frac{2L}{υ_0}$ | |
| D. | 若质子从bd方向入射,它在以后运动中电势能会先减小后增加 |
6.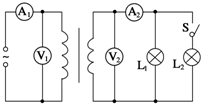 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
 为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )
为探究理想变压器原、副线圈电压、电流的关系,将原线圈接到电压有效值不变的正弦交流电源上,副线圈连接相同的灯泡L1、L2,电路中分别接了理想变流电压表V1、V2和理想交流电流表A1、A2,导线电阻不计,如图所示.当开关S闭合后( )| A. | A1示数变小,A1与A2示数的比值不变 | |
| B. | A1示数变大,A1与A2示数的比值变大 | |
| C. | V2示数变小,V1与V2示数的比值变大 | |
| D. | V2示数不变,V1与V2示数的比值不变 |