��Ŀ����
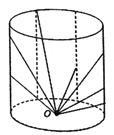
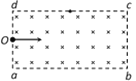
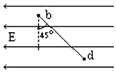
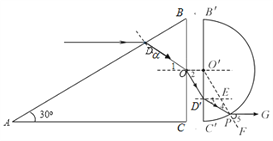
����Ŀ����2����ͼ��ʾ���뾶ΪR�İ�Բ�β���ש��һ��Ϊ30����Rt��ACB����שƽ�������Է��ã���O��O���ֱ���BC�ߵ��е�Ͱ�Բ�β���ש��Բ�ġ�һ��ƽ����AC�ߵĵ�ɫ���AB���ϵĵ�D���䣬�������ӵ�O��������Ӱ�Բ�β���ש�ϵ�ij��P�������֪BC����ֱ��B'C��������ȣ��������R/3����B��D�����ΪR�����ֲ���ש�ĺ���������ʾ���ͬ���������ǹ��ڸ�������ķ��䡣��
(i)����ש��������n��
(ii)��P��λ�ú͵�ɫ�������䷽��

���𰸡�![]() ,��
,��
 ����5=60��
����5=60��
��������(i)����DO����������BODǡΪ�ȱ������Σ��ɼ���֪ʶ����=30��
�ڽ���AB���������䶨�ɣ�sin60��=nsin��
n=![]()
(ii)���������·��ͼ��ʾ��
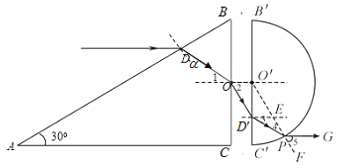
����O�㷢�����䣬 ![]() Ϊ���ߣ�
Ϊ���ߣ�
�������䶨���� ![]()
![]() 1=��=30��
1=��=30��
���![]() 2=60��
2=60��
����![]() �㷢�����䣬
�㷢�����䣬 ![]() Ϊ���ߣ��ɹ�·���棺
Ϊ���ߣ��ɹ�·���棺 ![]() 3=
3=![]() 1=30��
1=30��
��![]() ����
���� ![]()
��![]() �У��������Ҷ�����
�У��������Ҷ����� ![]()
���![]() 4=30��
4=30��
����P�㷢�����䣬�������䶨���� ![]()
��������� ![]() 5=60��������ƽ����
5=60��������ƽ����![]() �����������
�����������

��ϰ��ϵ�д�
�����Ŀ