题目内容
19.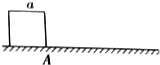 一个内部均匀的正方体物块的边长为a,质量为m,放在粗糙水平面上,如图所示.由于物块质量很大,摩擦力也很大,需要用以A为轴翻滚的方向向前移动物块,若移动距离为s,且s>a,问此人至少要对此物块做多少功?
一个内部均匀的正方体物块的边长为a,质量为m,放在粗糙水平面上,如图所示.由于物块质量很大,摩擦力也很大,需要用以A为轴翻滚的方向向前移动物块,若移动距离为s,且s>a,问此人至少要对此物块做多少功?
分析 正方体恰能绕O轴翻动时,地面对正方体除O点外没有支持力,以O为支点,当正方体的重心恰好上升到O点的正上方时,拉力做功最小.由功能关系求解.
解答 解:当正方体的重心恰好上升到O点的正上方时,拉力做功最小.由功能关系得:拉力做功至少为:
W=mgh=mg($\frac{\sqrt{2}}{2}a-\frac{1}{2}a$).
移动距离为s,且s>a,则需要的翻滚的次数:$n=\frac{s}{a}$
人做的总功:${W}_{总}=nW=nmg(\frac{\sqrt{2}}{2}a-\frac{1}{2}a)$=$\frac{mgs}{a}(\frac{\sqrt{2}}{2}a-\frac{1}{2}a)$=$\frac{(\sqrt{2}-1)mgs}{2}$
答:人至少要对此物块做功$\frac{(\sqrt{2}-1)mgs}{2}$.
点评 本题是临界问题,要抓住临界条件进行分析和求解.要使正方体能绕O轴翻动,只要使正方体的重心恰好上升到O点的正上方即可.

练习册系列答案
相关题目
10.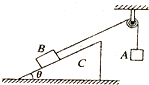 如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,则( )
如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,则( )
 如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,则( )
如图所示,倾角为θ的斜面体C置于水平面上,B置于斜面上,通过细绳跨过光滑的定滑轮与A相连接,连接B的一段细绳与斜面平行,A、B、C都处于静止状态,则( )| A. | B受到C的摩擦力一定不为零 | |
| B. | C受到水平面的摩擦力一定为零 | |
| C. | 不论B、C间摩擦力大小、方向如何,水平面对C的摩擦力方向一定向左 | |
| D. | 水平面对C的支持力大小等于B、C的重力之和 |
7. 图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依a→b→c→d→e轨迹运动.已知电势ΦK<ΦL<ΦM.下列说法中正确的是( )
图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依a→b→c→d→e轨迹运动.已知电势ΦK<ΦL<ΦM.下列说法中正确的是( )
 图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依a→b→c→d→e轨迹运动.已知电势ΦK<ΦL<ΦM.下列说法中正确的是( )
图中K、L、M为静电场中的三个相距很近的等势面(K、M之间无电荷).一带电粒子射入此静电场中后,依a→b→c→d→e轨迹运动.已知电势ΦK<ΦL<ΦM.下列说法中正确的是( )| A. | 粒子带负电 | B. | 粒子在bc段做减速运动 | ||
| C. | 粒子在b点与d点的速度相同 | D. | 粒子在c点时电势能最大 |
4. 如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
 如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )
如图所示,有一金属已知导体表面上A点附近的场强是导体表面上B点附近的场强的10倍.现有另一导体带有正电荷,带正电的点电荷分别从导体外侧距A、B点足够近处在电场力作用下,从静止起移到无穷远处(取无穷远处电势为零),则下列说法中错误的是( )| A. | 两次移动时电荷在初位置的加速度之比为10:1 | |
| B. | 两次移动过程电场力做功之比为1:1 | |
| C. | 移动过程中末速度之比为$\sqrt{10}$:1 | |
| D. | 导体上右端点A的电势等于左端点B的电势 |
18.关于绕地球运行的人造卫星,下列说法正确的是( )
| A. | 质量越大,离地面越远,速度越大 | |
| B. | 与质量无关,离地面越近,速度越大 | |
| C. | 人造卫星的运行速度大于等于7.9 km/s | |
| D. | 人造卫星的发射速度等于7.9 km/s |
 如图1所示,两根足够长平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,电阻与R1相等.导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.求:
如图1所示,两根足够长平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,电阻与R1相等.导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连.不计一切摩擦,不计导轨的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.求: 改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm.
改进后的“研究有固定转动轴物体平衡条件”的实验装置如图所示,力传感器、定滑轮固定在横杆上,替代原装置中的弹簧秤.已知力矩盘上各同心圆的间距为5cm. 如图所示,飞机距离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度为v2=15m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10m/s2)
如图所示,飞机距离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度为v2=15m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10m/s2)