题目内容
如图所示,将一根长为L的不可伸长的轻质绳子分成等长的两段,绳子的一端悬挂于水平天花板上,另一端共同吊起一个重力为G的物体P并处于静止状态,试求:

1.若绳子与天花板的夹角为θ,求绳子张力的大小;
2.若绳子的最大承受张力为T0=5G/6,要保证绳子不被拉断,求天花板上两悬挂点距离的取值要求。
【答案】
1.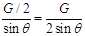
2.d ≤ 0.8L
【解析】(1)对物体P,其受力如图5所示 …………1分
物体P处于静止状态,其所受合力为零 …………1分
所以 T=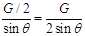 …………2分
…………2分
(2)由T= 可知,两悬挂点的距离越大,绳子的承受力就越大
…………1分
可知,两悬挂点的距离越大,绳子的承受力就越大
…………1分
当T= T0=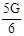 时,有
时,有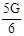 =
= …………1分
…………1分
所以sinθ=0.6…………1分
所以cosθ=0.8…………1分
设此时两悬挂点的距离为d0,有 =
=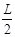
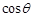 …………2分
…………2分
所以两悬挂点最大距离为d0=0.8L…………1分
天花板上两悬挂点距离的取值要求为d ≤ 0.8L…………1分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

