题目内容
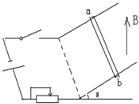
【题目】如图,截面为![]() 圆环的透明材料,O为该圆环的圆心,AB、CD是该圆环的两端,宽度均为d。单色光线a垂直AB从B点射入,光线恰好不从AD射出,而是从C点垂直CD射出。
圆环的透明材料,O为该圆环的圆心,AB、CD是该圆环的两端,宽度均为d。单色光线a垂直AB从B点射入,光线恰好不从AD射出,而是从C点垂直CD射出。
(1)求该透明材料的折射率;
(2)单色光线b与AB成45°从AB上的A点射入,已知光在真空中的传播速度为c。求光线b在该材料中的传播时间。

【答案】(1)![]() ;(2)
;(2)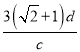
【解析】
(1)延长入射光线和反向延长出射光线交AD面的E点,如图
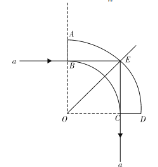
依题意光在E点发生全反射,∠BEO=45°为临界角,设该材料的折射率为n,则
sin∠BEO=![]()
解得
![]()
(2)过A作AB的法线,依题:入射角i=45°,设折射角为r,由
![]()
代入数据得
r=30°
光线传到AD面上的中,由几何光关系可知
∠AFO=60°>45°
则光在F处发生全反射,所以
∠OFP=60°
则FP垂直CD。如图所示,
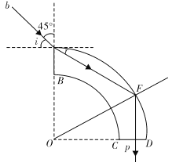
光线b在该材料中通过的路程为
AF+EP=![]() OD
OD
OD=OC+d
解得
OD=(2+![]() )d
)d
由于光线在材料中的传播速度为
![]()
光在材料中的传播时间
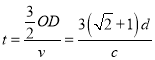

练习册系列答案
相关题目