题目内容
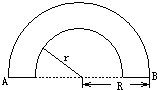 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 2 |
A、n可能为
| ||||
| B、n可能为1.2 | ||||
C、t可能为
| ||||
D、t可能为
|
分析:从A端口的最右边一点射入,发生两次全反射,垂直射出;结合光路的可逆性,作出光路图;由折射定律和几何知识结合求解.
解答:解:A、B、从A端口的最右边一点射入,发生两次全反射,结合光路的可逆性,作出光路图,如图所示:
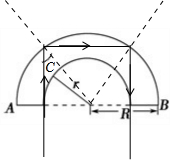
根据几何关系,有:
sinC=
=
=
故折射率的最小值为:n=
=1.414
故A正确,B错误;
C、D、图中光线的传播时间最短,光程为:S=2r+2r=4r;
光速为:v=
时间为:t=
由于:n≥
故t=
≥
,故C错误,D错误;
故选:A.

根据几何关系,有:
sinC=
| r |
| R |
| ||
| 2 |
| 1 |
| n |
故折射率的最小值为:n=
| 2 |
故A正确,B错误;
C、D、图中光线的传播时间最短,光程为:S=2r+2r=4r;
光速为:v=
| c |
| n |
时间为:t=
| s |
| v |
由于:n≥
| 2 |
| 4rn |
| c |
4
| ||
| c |
故选:A.
点评:本题考查全反射,解题的关键在于题目中几何关系的应用,只有根据几何关系解出临界角的正弦才能求出正确结果.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
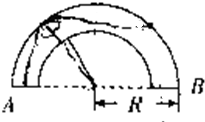 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 3 |
A、n可能为
| ||||
| B、n可能为2 | ||||
C、t可能为
| ||||
D、t可能为
|
 如图所示,空气中有一折射率为
如图所示,空气中有一折射率为 (2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
(2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=