题目内容
 如图所示,空气中有一折射率为
如图所示,空气中有一折射率为| 2 |
. |
| AB |
. |
| AB |
π
| R |
| 4 |
π
.| R |
| 4 |
分析:注意两条特殊光线,一是从O点沿半径方向进入玻璃柱体的光线,在AO面上折射后传播入方向不变,二是在AB面上发生全反射的光线,有光透出的部分在这两条光线之间,然后根据几何关系求解.
解答:解:根据折射定律有:
=
,可得光进入玻璃后光线与竖直方向的夹角为30°.
过O的光线垂直入射到AB界面上点C射出,C到B之间没有光线射出;越接近A的光线入射到AB界面上时的入射角越大,发生全反射的可能性越大.
根据临界角公式:sinC=
,得临界角为45°,如果AB界面上的临界点为D,此光线在AO界面上点E入射,在三角形ODE中可求得OD与水平方向的夹角为180°-(120°+45°)=15°,所以A到D之间没有光线射出.由此可得没有光线射出的圆弧对应圆心角为90°-(30°+15°)=45°
所以有光透出的部分的弧长为
πR.
故答案为:
πR.
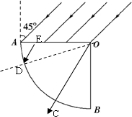
| sin45° |
| sinr |
| 2 |
过O的光线垂直入射到AB界面上点C射出,C到B之间没有光线射出;越接近A的光线入射到AB界面上时的入射角越大,发生全反射的可能性越大.
根据临界角公式:sinC=
| 1 | ||
|
所以有光透出的部分的弧长为
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |

点评:解决本题的关键根据光的折射、全反射原理在AB弧面上找到有光线透出的范围,然后依据几何关系求解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
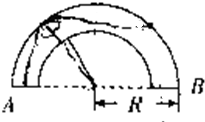 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 3 |
A、n可能为
| ||||
| B、n可能为2 | ||||
C、t可能为
| ||||
D、t可能为
|
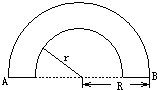 如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=| 2 |
A、n可能为
| ||||
| B、n可能为1.2 | ||||
C、t可能为
| ||||
D、t可能为
|
 (2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=
(2009?四川)如图所示,空气中有一横截面为半圆环的均匀透明柱体,其内圆半径为r,外圆半径为R,R=