题目内容
9. 参考信息:α粒子是氦的原子核,速度可达光速C的$\frac{1}{10}$,能使底片感光,但它的贯穿本领很小,一张普通的纸就能挡住它.β粒子是一种速度几乎可达光速C的电子,能穿透几毫米厚的铝板,能使底片感光.γ粒子是一种不带电的高能电磁波,贯穿本领很强,能穿透几厘米厚的铅板,能使底片感光.
参考信息:α粒子是氦的原子核,速度可达光速C的$\frac{1}{10}$,能使底片感光,但它的贯穿本领很小,一张普通的纸就能挡住它.β粒子是一种速度几乎可达光速C的电子,能穿透几毫米厚的铝板,能使底片感光.γ粒子是一种不带电的高能电磁波,贯穿本领很强,能穿透几厘米厚的铅板,能使底片感光.在暗窒的真空中做如下实验:在水平向外的匀强磁场中,有一个能产生α、β、γ三种射线的射线源,从射线源射出的一束射线垂直于磁场方向射入磁场,如图示,在与射线源距离为H处,水平放置两张叠放着的涂药面朝下的印像纸(比一般纸厚且韧的涂有感光药的纸),经射线照射一段时间后把两张印像纸显影.
(1)上面的印像纸有几个暗斑?各是什么射线的痕迹?
(2)求出α粒子和β粒子在磁场中运动的半径之比.
(3)若在此空间再加上与磁场方向垂直的匀强电场,一次使α射线不偏转,一次使β射线不偏转,则两次所加匀强电场的电场强度之比是多少?(已知mα=4u,mβ=$\frac{u}{1840}$)
分析 (1)一张普通的纸就能挡住α粒子;由此即可得出结论;
(2)根据洛伦兹力提供向心力,即可求出半径的比;
(3)当电场力与洛伦兹力大小相等,方向相反 时,粒子不发生偏转,由此即可求出.
解答 解:(1)由于一张普通的纸就能挡住α粒子,所以上面的印像纸有2个暗斑,一定是:一个是β射线的痕迹,另一个是γ射线的痕迹.
(2)根据洛伦兹力提供向心力,对于α粒子:2ev1B=${m}_{α}\frac{{v}_{1}^{2}}{{r}_{1}}$
对于β粒子:ev2B=${m}_{β}•\frac{{v}_{2}^{2}}{{r}_{2}}$
所以:$\frac{{r}_{1}}{{r}_{2}}=\frac{{m}_{α}{v}_{1}}{2{m}_{β}{v}_{2}}=\frac{4×u×0.1c}{2×\frac{u}{1840}×1{0}^{-30}×c}$=$\frac{368}{1}$
(2)若α粒子不偏转:2ev1B=2eE1
β粒子不偏转:ev2B=eE2
所以:$\frac{{E}_{1}}{{E}_{2}}=\frac{{v}_{1}}{{v}_{2}}=\frac{0.1c}{c}=\frac{1}{10}$
答:(1)上面的印像纸有2个暗斑,一个是β射线的痕迹,另一个是γ射线的痕迹;
(2)出α粒子和β粒子在磁场中运动的半径之比是$\frac{368}{1}$.
(3)若在此空间再加上与磁场方向垂直的匀强电场,一次使α射线不偏转,一次使β射线不偏转,则两次所加匀强电场的电场强度之比是$\frac{1}{10}$.
点评 本题综合性较强,主要考查两个方面的问题:①三种射线的成分主要是所带电性.②洛伦兹力的方向的判定.只有基础扎实,此类题目才能顺利解决,故要重视基础知识的学习.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 如图甲所示,一轻质弹簧的下端固定在水平面上,上端叠放两个质量均为M的物体A、B(B物体与弹簧连接),弹簧的劲度系数为k,初始时物体处于静止状态.现用竖直向上的拉力F用在物体A上,使物体A开始向上做加速度为a的匀加速运动,测得两个物体的v-r图象如图乙所示(重力加速度为g),则( )
如图甲所示,一轻质弹簧的下端固定在水平面上,上端叠放两个质量均为M的物体A、B(B物体与弹簧连接),弹簧的劲度系数为k,初始时物体处于静止状态.现用竖直向上的拉力F用在物体A上,使物体A开始向上做加速度为a的匀加速运动,测得两个物体的v-r图象如图乙所示(重力加速度为g),则( )| A. | 施加外力前,弹簧的形变量为2$\frac{Mg}{k}$ | |
| B. | 外力施加的瞬间,AB间的弹力大小为M(g-a) | |
| C. | AB在t1时刻分离,此时弹簧弹力恰好为零 | |
| D. | 弹簧恢复到原长时,物体B的速度达到最大值 |
| A. | 7N | B. | 3N | C. | 13N | D. | 9N |
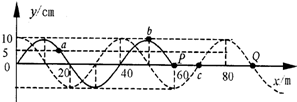 一列简谐横波沿X轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.7s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )
一列简谐横波沿X轴正方向传播,t时刻波形图如图中的实线所示,此时波刚好传到P点,t+0.7s时刻的波形如图中的虚线所示,a、b、c、P、Q是介质中的质点,则以下说法正确的是( )| A. | 这列波的波速可能为$\frac{300}{7}$m/s | |
| B. | 质点C在这段时间内通过的路程一定大于30cm | |
| C. | t+0.7s时P点的振动方向为Y轴正向 | |
| D. | 如果T=0.4s,则当t+0.5s时刻,质点b、P的位移相同 |
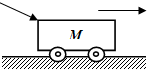
| A. | 力F对小车做正功 | B. | 力F对小车做负功 | C. | 合力做功为零 | D. | 以上说法都不对 |

| A. | 两车相遇 | B. | 两车速度大小相等,方向相反 | ||
| C. | 两车速度大小相等,方向相同 | D. | 两车的位移大小相等 |
 如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直:
如图所示,框架面积为S,框架平面与磁感应强度为B的匀强磁场方向垂直: 如图所示是电饭煲的电路图,S1是一个控温开关,手动闭合后,当此开关温度达到103℃时,会自动断开,S2是一个自动控温开关,当温度低于70℃时,会自动闭合;温度高于80℃时,会自动断开.红灯是加热时的指示灯,黄灯是保温时的指示灯,定值电阻R1=R2=500Ω,加热电阻丝R3=50Ω,两灯电阻不计.
如图所示是电饭煲的电路图,S1是一个控温开关,手动闭合后,当此开关温度达到103℃时,会自动断开,S2是一个自动控温开关,当温度低于70℃时,会自动闭合;温度高于80℃时,会自动断开.红灯是加热时的指示灯,黄灯是保温时的指示灯,定值电阻R1=R2=500Ω,加热电阻丝R3=50Ω,两灯电阻不计.