题目内容
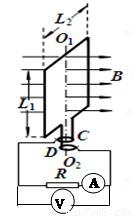
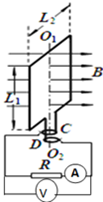 如图所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小开始时随时间t不断增大,关系式为B=B0+
如图所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小开始时随时间t不断增大,关系式为B=B0+| △Φ |
| △t |
| nL1L2(B1-B0) |
| t1 |
(1)0~t1时间内电流表A的示数;
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量;
(3)线框匀速转动后,从图甲所示位置转过90°的过程中,电压表V的示数和通过电阻R的电荷量.
分析:(1)根据法拉第电磁感应定律,结合闭合电路欧姆定律,即可求解;
(2)根据线框产生最大感应电动势,结合正弦交流电有效值与最大值的关系,依据焦耳定律,即可求解;
(3)根据法拉第电磁感应定律,求出平均感应电动势,从而根据电量q=
t,即可求解.
(2)根据线框产生最大感应电动势,结合正弦交流电有效值与最大值的关系,依据焦耳定律,即可求解;
(3)根据法拉第电磁感应定律,求出平均感应电动势,从而根据电量q=
. |
| I |
解答:解:(1)0~t1时间内,线框中的感应电动势为E=n
=
,
根据闭合电路欧姆定律可知,通过电阻R的电流即为A表示数I=
=
.
(2)线框产生感应电动势的最大值 Em=nB1 L1L2ω,
感应电动势的有效值E=
nB1 L1L2ω,
通过电阻R的电流的有效值I=
,
线框转动一周所需的时间t=
,
此过程中,电阻R产生的热量 Q=I2Rt=πRω(
)2.
(3)线框从图甲所示位置转过90°的过程中,由(2)可知,电压表示数U=
,
该过程中平均感应电动势,
=
=
,
平均感应电流,
=
,
通过电阻R的电荷量,q=
?△t=
.
答:(1)0~t1时间内电流表A的示数为
;
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量πRω(
)2;
(3)线框匀速转动后,从图甲所示位置转过90°的过程中,电压表V的示数
,和通过电阻R的电荷量
.
| △Φ |
| △t |
| nL1L2(B1-B0) |
| t1 |
根据闭合电路欧姆定律可知,通过电阻R的电流即为A表示数I=
| E |
| R+r |
| nL1L2(B1-B0) |
| (R+r)t1 |
(2)线框产生感应电动势的最大值 Em=nB1 L1L2ω,
感应电动势的有效值E=
| ||
| 2 |
通过电阻R的电流的有效值I=
| ||
| 2(R+r) |
线框转动一周所需的时间t=
| 2π |
| ω |
此过程中,电阻R产生的热量 Q=I2Rt=πRω(
| nB1L1L2 |
| R+r |
(3)线框从图甲所示位置转过90°的过程中,由(2)可知,电压表示数U=
| ||
| 2(R+r) |
该过程中平均感应电动势,
. |
| E |
| n△? |
| △t |
| nB1L1L2 |
| △t |
平均感应电流,
. |
| I |
| nB1L1L2 |
| △t(R+r) |
通过电阻R的电荷量,q=
. |
| I |
| nB1L1L2 |
| R+r |
答:(1)0~t1时间内电流表A的示数为
| nL1L2(B1-B0) |
| (R+r)t1 |
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量πRω(
| nB1L1L2 |
| R+r |
(3)线框匀速转动后,从图甲所示位置转过90°的过程中,电压表V的示数
| ||
| 2(R+r) |
| nB1L1L2 |
| R+r |
点评:考查法拉第电磁感应定律、闭合电路欧姆定律与焦耳定律的应用,注意正弦交流电的最大值与有效值及平均值如何求解,同时知道电表的示数表交流电的有效值.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
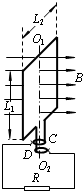 如图所示,长、宽分别为L1=0.05m、L2=0.04m的矩形金属线框位于竖直平面内,其匝数为n=400,总电阻为r=1Ω,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D焊接在一起,并通过电刷和一个R=9Ω的定值电阻相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B=0.25T.线框从图示位置(线框平面和磁场垂直)开始在外力的驱动下绕其竖直中心轴以角速度ω=l00rad/s匀速转动.求:
如图所示,长、宽分别为L1=0.05m、L2=0.04m的矩形金属线框位于竖直平面内,其匝数为n=400,总电阻为r=1Ω,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D焊接在一起,并通过电刷和一个R=9Ω的定值电阻相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B=0.25T.线框从图示位置(线框平面和磁场垂直)开始在外力的驱动下绕其竖直中心轴以角速度ω=l00rad/s匀速转动.求: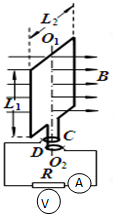 如图所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度大小为B.线框在外力的驱动下绕其竖直中心轴以角速度ω匀速转动.
如图所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度大小为B.线框在外力的驱动下绕其竖直中心轴以角速度ω匀速转动.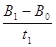 t,当t=t1时刻后保持B1不变,其中B0、B1和t1均为已知。在0~t1的时间内,若保持线框静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。
t,当t=t1时刻后保持B1不变,其中B0、B1和t1均为已知。在0~t1的时间内,若保持线框静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。
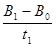 t,当t=t1时刻后保持B1不变,其中B0、B1和t1均为已知。在0~t1的时间内,若保持线框静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。
t,当t=t1时刻后保持B1不变,其中B0、B1和t1均为已知。在0~t1的时间内,若保持线框静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动。