题目内容
【题目】为减少烟尘排放对空气的污染，某同学设计了一个如图所示的静电除尘器，该除尘器的上下底面是边长为L＝0.20m的正方形金属板，前后面是绝缘的透明有机玻璃，左右面是高h＝0.10m的通道口。使用时底面水平放置，两金属板连接到U＝2000V的高压电源两极（下板接负极），于是在两金属板间产生一个匀强电场（忽略边缘效应）。均匀分布的带电烟尘颗粒以v=10m/s的水平速度从左向右通过除尘器，已知每个颗粒带电荷量q＝+2.0×10-17C，质量m＝1.0×10-15kg，不考虑烟尘颗粒之间的相互作用和空气阻力，并忽略烟尘颗粒所受重力。在闭合开关后：
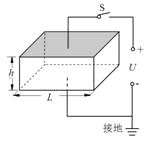
（1）求烟尘颗粒在通道内运动时加速度的大小和方向；
（2）求除尘过程中烟尘颗粒在竖直方向所能偏转的最大距离；
（3）除尘效率是衡量除尘器性能的一个重要参数。除尘效率是指一段时间内被吸附的烟尘颗粒数量与进入除尘器烟尘颗粒总量的比值。试求在上述情况下该除尘器的除尘效率；若用该除尘器对上述比荷的颗粒进行除尘，试通过分析给出在保持除尘器通道大小不变的前提下，提高其除尘效率的方法。
【答案】（1）
方向竖直向下 （2）8.0cm；（3）在除尘器通道大小及颗粒比荷不改变的情况下，可以通过适当增大两金属板间的电压U，或通过适当减小颗粒进入通道的速度v来提高除尘效率。
【解析】
试题分析：（1）烟尘颗粒在通道内只受电场力的作用，电场力F=qE （1分）
又因为 
（1分）
设烟尘颗粒在通道内运动时加速度为a，根据牛顿第二定律有 
（2分）
解得 ，方向竖直向下 （2分）
（2）若通道最上方的颗粒能通过通道，则这些颗粒在竖直方向上有最大的偏转距离
这些颗粒在水平方向的位移 L=vt （2分）
在竖直方向的位移 
（2分）
解得 
可确定这些颗粒能通过通道
因此，除尘过程中烟尘颗粒在竖直方向偏转的最大距离为8.0cm （2分）
（3）设每立方米有烟尘颗粒为N0
时间t内进入除尘器的颗粒N1= N0hLvt （1分）
时间t内吸附在底面上的颗粒N2= N0h0Lvt （1分）
则除尘效率 
=80％ （2分）
因为
当h0<h时，
当h0≥h时，η=1 （2分）
因此，在除尘器通道大小及颗粒比荷不改变的情况下，可以通过适当增大两金属板间的电压U，或通过适当减小颗粒进入通道的速度v来提高除尘效率。 （2分）
