题目内容
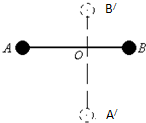 如图所示,一根长为3l,可绕O轴在竖直平面内无摩擦转动的细杆AB,已知OA=2l,OB=l,质量相等的两个球分别固定在杆的A、B端,由水平位置自由释放,求轻杆转到竖直位置时两球的速度分别为多大?
如图所示,一根长为3l,可绕O轴在竖直平面内无摩擦转动的细杆AB,已知OA=2l,OB=l,质量相等的两个球分别固定在杆的A、B端,由水平位置自由释放,求轻杆转到竖直位置时两球的速度分别为多大?分析:因A、B两球用轻杆相连,故两球转动的角速度相等,对A、B两球组成的系统应用机械能守恒定律即可解题.
解答:解:A、B两球转动的角速度相等,故
=
;
对A、B两球组成的系统应用机械能守恒定律,得到
mg?2L-mgL=
m
+
m
解得
vA=2
vB=
答:轻杆转到竖直位置时A球的速度为2
,B球的速度为
.
| vA |
| vB |
| 2 |
| 1 |
对A、B两球组成的系统应用机械能守恒定律,得到
mg?2L-mgL=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
解得
vA=2
|
vB=
|
答:轻杆转到竖直位置时A球的速度为2
|
|
点评:本题关键是A、B球机械能均不守恒,但A与B系统机械能守恒,根据守恒定律列式求解即可.

练习册系列答案
相关题目
 (2012?杨浦区一模)如图所示,一根长为三的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和mb,杆可绕距a球为L/4处的水平定轴D在竖直平面内转动,初始时杆处于竖直位置,小球b几乎接触桌面,在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面.现用一水平恒力F作用于a球上,使之绕O轴逆时针转动,设在此过程中立方体物块没有发生转动,且小球b立方体物块始终接触没有分离.不计一切摩擦,求:
(2012?杨浦区一模)如图所示,一根长为三的细刚性轻杆的两端分别连结小球a和b,它们的质量分别为ma和mb,杆可绕距a球为L/4处的水平定轴D在竖直平面内转动,初始时杆处于竖直位置,小球b几乎接触桌面,在杆的右边水平桌面上,紧挨着细杆放着一个质量为m的立方体匀质物块,图中ABCD为过立方体中心且与细杆共面的截面.现用一水平恒力F作用于a球上,使之绕O轴逆时针转动,设在此过程中立方体物块没有发生转动,且小球b立方体物块始终接触没有分离.不计一切摩擦,求: (2013?滨州一模)如图所示,一根长为L=5m的轻绳一端固定在 O′点,另一端系一质量m=1kg的小球(小球可视为质点).将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点O时,轻绳刚好被拉断.O点下方有一以O点为圆心,半径
(2013?滨州一模)如图所示,一根长为L=5m的轻绳一端固定在 O′点,另一端系一质量m=1kg的小球(小球可视为质点).将轻绳拉至水平并将小球由位置A静止释放,小球运动到最低点O时,轻绳刚好被拉断.O点下方有一以O点为圆心,半径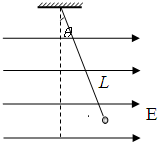 如图所示,一根长为L的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场当中,电场强度大小为E,方向是水平向右,已知:当细线偏离竖直方向为θ角时,小球处于平衡状态,试求:
如图所示,一根长为L的细绝缘线,上端固定,下端系一个质量为m的带电小球,将整个装置放入一匀强电场当中,电场强度大小为E,方向是水平向右,已知:当细线偏离竖直方向为θ角时,小球处于平衡状态,试求: 为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求:
为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求:
 为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求:
为0.8m的细绳,一端拴一个质量为m的小球,另一端悬于离地面高h为2.6m处,当细绳受到3mg拉力时会被拉断,现把这小球拉到使细绳与竖直方向夹角为θ时由静止释放,若球摆到细绳竖直位置时,绳子刚好被拉断,小球平抛落到地面。求: