题目内容
9.一辆火车以速度v相对地面运动,在车厢的正中点装有一盏闪光灯,当它闪光时,有两个光子分别从左右传播,在火车的前后两端装有设备,使坐在车中的观察者能测知这两个光子何时到达两端,通过某种巧妙的装置,静止在地面上的另一观察者也能测知这两个光子的传播过程,若车厢长为l,则:(1)车厢内的观察者测得两光子从闪光开始到达前后端各需要多少时间?时间差为多少?
(2)静止于地面的观察者测得两光子从闪光开始到达前后端,各需要多少时间?时间差为多少?
分析 (1)车厢内的人与火车具有相同的速度,光相对于人的速度为光速,结合运动学的公式即可解答;
(2)静止于地面的观察者观察到光相对于人的速度为光速,但是由于火车的运动,光到达两侧的时间是不相同的,由运动学的公式即可求出.
解答 解:(1)车厢内的人与火车具有相同的速度,光相对于人的速度为光速,所以光子到达前后端是时间都是:$\frac{\frac{l}{2}}{c}=\frac{l}{2c}$,所以时间差是0;
(2)静止于地面的观察者观察到光相对于人的速度为光速,但是由于火车的运动,他们的位移不同,设静止在地面上的观察者开始时的位置在车行道中点,人观察到光子到达前端的时间为t1,光子到达后端的时间为t2,则:$c{t}_{1}=\frac{1}{2}l+v{t}_{1}$,$c{t}_{2}=\frac{1}{2}l-v{t}_{2}$
所以:${t}_{1}=\frac{l}{2(c-v)}$,${t}_{2}=\frac{l}{2(c+v)}$
时间差:$△t={t}_{1}-{t}_{2}=\frac{l}{(c-v)(c+v)}$
答:(1)车厢内的观察者测得两光子从闪光开始到达前后端都需要,$\frac{l}{2c}$,时间差为0;
(2)静止于地面的观察者测得两光子从闪光开始到达前后端,各需要$\frac{l}{2(c-v)}$,和$\frac{l}{2(c+v)}$时间,时间差为 $\frac{l}{(c-v)(c+v)}$.
点评 地面上的人、车厢中的人选择的惯性系不一样,但是光向前传播和向后传播的速度相同,从而发现传播到前后壁的快慢不一样.地面上的人、车厢中的人选择的惯性系不一样,则观察到的现象不同,属于爱因斯坦相对性原理.

练习册系列答案
相关题目
19.在世界摩托车锦标赛中,有的赛车在水平路面上转弯时,常常在弯道上冲出跑道,原因是( )
| A. | 赛车冲出跑道是由于赛车行驶到弯道时,受到的向心力过大 | |
| B. | 赛车冲出跑道是由于赛车行驶到弯道时,运动员没有及时加速 | |
| C. | 赛车冲出跑道是由于赛车行驶到弯道时,运动员没有及时减速 | |
| D. | 由公式F=mω2r可知,弯道半径越大,越容易冲出跑道 |
20.磁电式仪表的线圈常用铝框做骨架,把线圈绕在铝框上而不用塑料做骨架是因为( )
| A. | 塑料材料的坚硬程度达不到要求 | |
| B. | 在铝框和指针一起摆动时更容易使指针很快停止摆动 | |
| C. | 其它相同下,在通电后铝框比塑料框更容易摆动起来 | |
| D. | 塑料是绝缘体,塑料框和指针一起摆动时更容易使指针很快停止摆动 |
17.假设一个小型宇宙飞船沿人造地球卫星的轨道在高空中绕地球做匀速圆周运动,如果飞船沿其速度相反的方向抛出一个质量不可忽略的物体A,则下列说法正确的是( )
| A. | A与飞船都可能沿原轨道运动 | |
| B. | A与飞船都不可能沿原轨道运动 | |
| C. | A运动的轨道半径可能减小,也可能增加 | |
| D. | A可能沿地球半径方向竖直下落,而飞船运行的轨道半径将增大 |
4.精彩的F1赛事相信你不会陌生吧!车王舒马赫在2005年以8000万美元的年收入高居全世界所有运动员榜首.在观众感觉精彩与刺激的同时,车手们却时刻处在紧张与危险之中.这位车王在一个弯道上突然高速行驶的赛车后轮脱落,从而不得不遗憾地退出了比赛.关于脱落的后轮的运动情况,以下说法正确的是( )
| A. | 仍然沿着汽车行驶的弯道运动 | |
| B. | 沿着与弯道垂直的方向飞出 | |
| C. | 沿着脱离时,轮子前进的方向做直线运动,离开弯道 | |
| D. | 上述情况都有可能 |
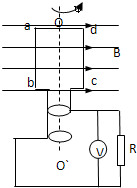 如图所示,匀强磁场的磁感应强度B=1T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=4π rad/s,外电路电阻R=3Ω,求:
如图所示,匀强磁场的磁感应强度B=1T,边长L=10cm的正方形线圈abcd共100匝,线圈电阻r=1Ω,线圈绕垂直于磁感线的对称轴OO′匀速转动,角速度ω=4π rad/s,外电路电阻R=3Ω,求:



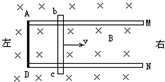 质量为m的金属棒bc长l,在两水平放置的平行光滑金属导轨上由静止匀加速运动t时,速度为v,闭合回路AbcD中bc棒将受到向向左的磁场力;其大小是$\frac{{B}^{2}{L}^{2}v}{R}$.为使bc棒向右运动,必须对bc施加方向向右,大小为$\frac{{B}^{2}{L}^{2}v}{R}+\frac{mv}{t}$的力,这个力克服安培力做功;在这个过程中机械能能转化成了电能.该时间内通过bc棒中的电量是$\frac{Blvt}{R}$(回路中总电阻为R).
质量为m的金属棒bc长l,在两水平放置的平行光滑金属导轨上由静止匀加速运动t时,速度为v,闭合回路AbcD中bc棒将受到向向左的磁场力;其大小是$\frac{{B}^{2}{L}^{2}v}{R}$.为使bc棒向右运动,必须对bc施加方向向右,大小为$\frac{{B}^{2}{L}^{2}v}{R}+\frac{mv}{t}$的力,这个力克服安培力做功;在这个过程中机械能能转化成了电能.该时间内通过bc棒中的电量是$\frac{Blvt}{R}$(回路中总电阻为R).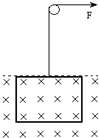 如图所示,某矩形线圈长为L、宽为d、匝数为n、总质量为M,其电阻为R,线圈所在磁场的磁感应强度为B,最初时刻线圈的上边缘与有界磁场上边缘重合,若将线圈从磁场中以速度v匀速向上拉出,则:
如图所示,某矩形线圈长为L、宽为d、匝数为n、总质量为M,其电阻为R,线圈所在磁场的磁感应强度为B,最初时刻线圈的上边缘与有界磁场上边缘重合,若将线圈从磁场中以速度v匀速向上拉出,则: