题目内容
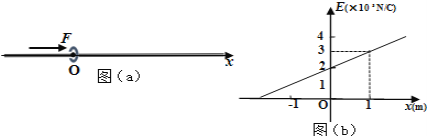
【题目】一光滑绝缘细直长杆处于静电场中,沿细杆建立坐标轴x,以x=0处的O点为电势零点,如图(a)所示.细杆各处电场方向沿x轴正方向,其电场强度E随x的分布如图(b)所示.细杆上套有可视为质点的带电环,质量为m=0.2kg,电荷量为q=-2.0×10-6C.带电环受沿x轴正向的恒力F=1.0N的作用,从O点静止开始运动,求:
(1)带电环在x=1m处的加速度;
(2)带电环运动区间内的电势最低值;
(3)带电环动能为0.5J时的位置;
【答案】(1)2 m/s2 方向水平向右;(2)-3×106V;(3)1m 或 5m;
【解析】试题分析:
(1)由图象得到电场强度随时间变化的函数表达式,求出在x=1m处的合力,根据牛顿第二定律求解;
(2)由动能定理求得当带电环运动区间内的电势最低值的距离,在结合图象可求;(3)由动能定理求得带电环动能为0.5J时的位置;
(1) 由图可知:E=(x+2)×105N/C,可知
带电环受到的电场力:FE=Eq=(x+2)×10-5×2×10-6=0.2x+0.4 N
带电环受到的合外力:F合=F-Eq=1-(0.2x+0.4)N=0.6-0.2x
当x=1m时,F合=0.6-0.2x=(0.6-0.2)N=0.4N
由F=ma得: ![]() ;
;
(2) 因为沿电场线方向电势降低,所以当带电环沿x轴正方向运动到了最远处电势最低点,
由动能定理得:
解得x=6m
由E-x图象可知:U0-Umin=0-[(2+8)×105×6]/2=-3×106V ;
(3) 当W合=0.5J时,带电环动能为0.5J,由![]()
解得x=1m或x=5m。

练习册系列答案
相关题目