题目内容
如图,光滑水平面上有一质量M=4.0kg的带有圆弧轨道的平板车,车的上表面是一段长L=1.5m的粗糙水平轨道,水平轨道左侧连一半径R=0.25m的四分之一光滑圆弧轨道,圆弧轨道与水平轨道在O′点相切.现将一质量m=1.0kg的小物块(可视为质点)从平板车的右端以水平向左的初速度v0滑上平板车,小物块与水平轨道间的动摩擦因数μ=0.5,小物块恰能到达圆弧轨道的最高点A.取g=10m/s2,求:
(1)小物块滑上平板车的初速度v0的大小.
(2)小物块与车最终相对静止时,它距O′点的距离.

(1)小物块滑上平板车的初速度v0的大小.
(2)小物块与车最终相对静止时,它距O′点的距离.

(1)平板车和小物块组成的系统水平方向动量守恒,设小物块到达圆弧最高点A时,二者的共同速度,
规定向左为正方向,由动量守恒得:mv0=(M+m)v1…①
由能量守恒得:
m
-
(M+m)
=mgR+μmgL…②
联立①②并代入数据解得:v0=5m/s…③
(2)设小物块最终与车相对静止时,二者的共同速度v2,从小物块滑上平板车,到二者相对静止的过程中,规定向左为正方向,由动量守恒得:
mv0=(M+m)v2…④
设小物块与车最终相对静止时,它距O′点的距离为x.由能量守恒得:
m
-
(M+m)
=μmg(L+x)…⑤
联立③④⑤并代入数据解得:x=0.5m
答:(1)小物块滑上平板车的初速度v0的大小是5m/s.
(2)小物块与车最终相对静止时,它距O′点的距离是0.5m.
规定向左为正方向,由动量守恒得:mv0=(M+m)v1…①
由能量守恒得:
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 21 |
联立①②并代入数据解得:v0=5m/s…③
(2)设小物块最终与车相对静止时,二者的共同速度v2,从小物块滑上平板车,到二者相对静止的过程中,规定向左为正方向,由动量守恒得:
mv0=(M+m)v2…④
设小物块与车最终相对静止时,它距O′点的距离为x.由能量守恒得:
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
| v | 22 |
联立③④⑤并代入数据解得:x=0.5m
答:(1)小物块滑上平板车的初速度v0的大小是5m/s.
(2)小物块与车最终相对静止时,它距O′点的距离是0.5m.

练习册系列答案
相关题目




 飞行的子弹分别穿透两块由同种材料制成的固定木板,若子弹穿透木板后的速度分别是0.6
飞行的子弹分别穿透两块由同种材料制成的固定木板,若子弹穿透木板后的速度分别是0.6

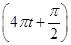 m
m m
m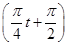 m
m