题目内容
质量为10kg的木箱,向右以初速度6m/s做匀减速直线运动,已知木箱与地面动摩擦因数为0.2,求(1)木箱的加速度的大小及方向?(2)经过多长时间停下来?(3)共向右运动了多长距离?(重力加速度g取10m/s2)
分析:(1)木箱受到三个力作用:重力、地面的支持力和滑动摩擦力,重力与支持力平衡,根据牛顿第二定律求解加速度大小和方向.
(2)由速度公式求解滑行的时间.
(3)由位移公式求解滑行的距离.
(2)由速度公式求解滑行的时间.
(3)由位移公式求解滑行的距离.
解答:解:(1)取向右为正方向
则f=-μFN=-μmg
根据牛顿第二定律得f=ma
代入解得a=-gμ=-10m/s2?0.2=-2m/s2,即木箱的加速度的大小为2m/s2,方向水平向左.
(2)由v=v0+at得 t=
=
s=3s
(3)x=
t=
t=9m
答:(1)木箱的加速度的大小为2m/s2,方向水平向左.
(2)经过3s时间停下来.
(3)共向右运动了9m距离.
则f=-μFN=-μmg
根据牛顿第二定律得f=ma
代入解得a=-gμ=-10m/s2?0.2=-2m/s2,即木箱的加速度的大小为2m/s2,方向水平向左.
(2)由v=v0+at得 t=
| v-v0 |
| a |
| 0-6 |
| -2 |
(3)x=
. |
| v |
| v0+ v |
| 2 |
答:(1)木箱的加速度的大小为2m/s2,方向水平向左.
(2)经过3s时间停下来.
(3)共向右运动了9m距离.
点评:本题是简单的动力学问题,应用牛顿第二定律和运动学公式结合求解是最基本的方法.

练习册系列答案
相关题目
如图甲所示,一人用由零逐渐增大的水平力F推静止于水平地面上、质量为10kg的木箱,木箱与水平地面间的摩擦力f与N的关系如图一所示,取g=10m/s2,可知( )
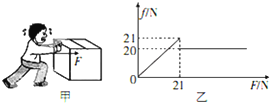

| A、木箱所受的最大静摩擦力为fm=20N | B、木箱所受的最大静摩擦力为fm=21N | C、木箱与地面间的动摩擦因数为μ=0.20 | D、木箱与地面间的动摩擦因数为μ=0.21 |
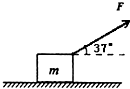 如图所示,一个质量为10kg的木箱放在水平面上,木箱与水平面间的动摩擦因数为0.5.现有一个与水平方向成37°角的恒力F=50N作用下,从静止开始作匀加速直线运动,4秒后撤去外力F,求:
如图所示,一个质量为10kg的木箱放在水平面上,木箱与水平面间的动摩擦因数为0.5.现有一个与水平方向成37°角的恒力F=50N作用下,从静止开始作匀加速直线运动,4秒后撤去外力F,求: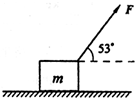 (2007?南京模拟)如图所示,一个质量为10kg的木箱放在水平面上,木箱与水平面间的动摩擦因数为0.5.现有一个与水平方向成53°角的拉力拉着木箱沿水平方向以4m/s速度匀速前进,求:
(2007?南京模拟)如图所示,一个质量为10kg的木箱放在水平面上,木箱与水平面间的动摩擦因数为0.5.现有一个与水平方向成53°角的拉力拉着木箱沿水平方向以4m/s速度匀速前进,求: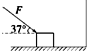 如图所示,水平面上质量为10kg的木箱与墙角距离为23
如图所示,水平面上质量为10kg的木箱与墙角距离为23