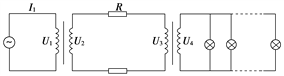
题目内容
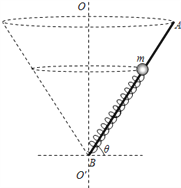
【题目】如图所示，光滑杆AB长为L=3m，B端固定一根劲度系数为k=10N/m、原长为L0=2m的轻弹簧，质量为m=2kg的小球套在光滑杆上并与弹簧的上端连接． 
为过B点的竖直轴，杆与水平面间的夹角始终为θ=53°．
（1）当球随杆一起绕
轴匀速转动时，弹簧恰好处于原长，求匀速转动时的角速度ω；
（2）球随杆在第(1)小题的角速度下匀速转动，球突然获得沿杆向上的一个分速v=3m/s，小球恰好能沿杆运动到最高点A，求小球从开始滑动到杆的最高点过程中，杆对球所做的功W．（已知：弹簧的弹性势能大小
，其中x为弹簧的形变量）
【答案】（1）
（2）32J
【解析】试题分析： 对小球分析，抓住竖直方向上的合力为零，水平方向上的合力提供向心力，列式联立求出匀速转动的角速度；根据牛顿第二定律求出小球做匀速转动时距离B点的距离，求出此时小球的动能，结合最高点的动能，运用动能定理求出杆对小球做功的大小。
（1）当弹簧恢复原长时，由牛顿第二定律可得：
代入数据解得： 
刚开始滑动时，垂直于杆的分速度
，
沿杆方向速度
所以开始滑动时的初速度
最高点时的速度
向上滑动过程中，弹簧弹力做的功
重力做的功
滑动过程运用动能定理： 
得W=32J
练习册系列答案
阅读快车系列答案
相关题目
