题目内容
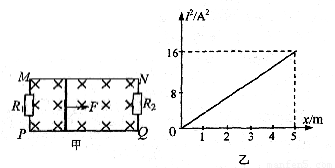
 如图甲所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小随时间t的变化关系如图乙所示,其中B0、B1和t1均为已知.在0~t1的时间内,线框保持静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动.求:
如图甲所示,长、宽分别为L1、L2的矩形金属线框位于竖直平面内,其匝数为n,总电阻为r,可绕其竖直中心轴O1O2转动.线框的两个末端分别与两个彼此绝缘的铜环C、D(集流环)焊接在一起,并通过电刷和定值电阻R相连.线框所在空间有水平向右均匀分布的磁场,磁感应强度B的大小随时间t的变化关系如图乙所示,其中B0、B1和t1均为已知.在0~t1的时间内,线框保持静止,且线框平面和磁场垂直;t1时刻后线框在外力的驱动下开始绕其竖直中心轴以角速度ω匀速转动.求:(1)0~t1时间内通过电阻R的电流大小;
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量;
(3)线框匀速转动后,从图甲所示位置转过90°的过程中,通过电阻R的电荷量.
(4)当线圈平面与中性面夹角为π/3时,感应电动势为多少?
分析:(1)根据法拉第电磁感应定律求出0~t1时间内感应电动势,再根据闭合电路欧姆定律求出通过电阻R的电流大小.
(2)根据E=nBSω求出感应电动势的最大值,从而求出感应电动势的有效值,根据欧姆定律求出感应电流的有效值,从而根据Q=I2Rt求出电阻R产生的热量.
(3)根据法拉第电磁感应定律结合闭合电路欧姆定律求出平均感应电流,根据q=
t求出通过电阻R的电荷量.
(4)通过从中性面开始计时感应电动势的表达式,求出线圈平面与中性面夹角为
时,感应电动势的大小.
(2)根据E=nBSω求出感应电动势的最大值,从而求出感应电动势的有效值,根据欧姆定律求出感应电流的有效值,从而根据Q=I2Rt求出电阻R产生的热量.
(3)根据法拉第电磁感应定律结合闭合电路欧姆定律求出平均感应电流,根据q=
. |
| I |
(4)通过从中性面开始计时感应电动势的表达式,求出线圈平面与中性面夹角为
| π |
| 3 |
解答:解:(1)0~t1时间内,线框中的感应电动势E=n
=
.
根据闭合电路欧姆定律得,通过电阻R的电流
I=
=
(2)线框产生的感应电动势的最大值Em=nB1L1L2ω
感应电动势的有效值E=
nB1L1L2ω
通过电阻R的电流有效值I=
线框转动一周所需的时间t=
.
此过程中,电阻R产生的热量Q=I2Rt=πRω(
)2.
(3)线框从图甲所示位置转过90°的过程中,
平均感应电动势
=n
=
平均感应电流
=
流过电阻R的电荷量q=
△t=
.
(4)从中性面开始计时感应电动势的瞬时表达式为E=Emsinωt
当线圈平面与中性面夹角为
时,即ωt=
,则E=
nB1L1L2ω.
答:(1)0~t1时间内通过电阻R的电流大小为
.
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量为πRω(
)2.
(3)通过电阻R的电荷量为
.
(4)当线圈平面与中性面夹角为π/3时,感应电动势为
nB1L1L2ω.
| △Φ |
| △t |
| nL1L2(B1-B0) |
| t1 |
根据闭合电路欧姆定律得,通过电阻R的电流
I=
| E |
| R+r |
| nL1L2(B1-B0) |
| (R+r)t1 |
(2)线框产生的感应电动势的最大值Em=nB1L1L2ω
感应电动势的有效值E=
| ||
| 2 |
通过电阻R的电流有效值I=
| ||
| 2(R+r) |
线框转动一周所需的时间t=
| 2π |
| ω |
此过程中,电阻R产生的热量Q=I2Rt=πRω(
| nB1L1L2 |
| R+r |
(3)线框从图甲所示位置转过90°的过程中,
平均感应电动势
. |
| E |
| △Φ. |
| △t |
| nB1L1L2 |
| △t |
平均感应电流
. |
| I |
| nB1L1L2 |
| △t(R+r) |
流过电阻R的电荷量q=
. |
| I |
| nB1L1L2 |
| R+r |
(4)从中性面开始计时感应电动势的瞬时表达式为E=Emsinωt
当线圈平面与中性面夹角为
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
答:(1)0~t1时间内通过电阻R的电流大小为
| nL1L2(B1-B0) |
| (R+r)t1 |
(2)线框匀速转动后,在转动一周的过程中电流通过电阻R产生的热量为πRω(
| nB1L1L2 |
| R+r |
(3)通过电阻R的电荷量为
| nB1L1L2 |
| R+r |
(4)当线圈平面与中性面夹角为π/3时,感应电动势为
| ||
| 2 |
点评:解决本题的关键掌握感应电动势的平均值、最大值、有效值和瞬时值的区别以及应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
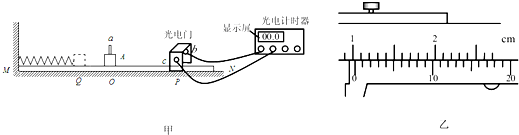


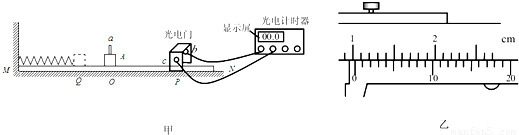
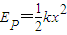 (其中k为弹簧的劲度系数,x为弹簧的形变量).他们设计了一种装置用于在航天飞机中测物体的质量,具体的方法如图甲所示,A是待测质量的小铁块,MN是平行航天飞机地板的平面,a为固定在小铁块上的挡光条,b、c 分别是光电门的激光发射和接收装置(当有物体从 b、c间通过时,光电计时器就可以显示物体的挡光时间).另有一把游标卡尺、一把毫米刻度尺、已知劲度系数为k的轻弹簧,他们设计的实验步骤如下:
(其中k为弹簧的劲度系数,x为弹簧的形变量).他们设计了一种装置用于在航天飞机中测物体的质量,具体的方法如图甲所示,A是待测质量的小铁块,MN是平行航天飞机地板的平面,a为固定在小铁块上的挡光条,b、c 分别是光电门的激光发射和接收装置(当有物体从 b、c间通过时,光电计时器就可以显示物体的挡光时间).另有一把游标卡尺、一把毫米刻度尺、已知劲度系数为k的轻弹簧,他们设计的实验步骤如下: