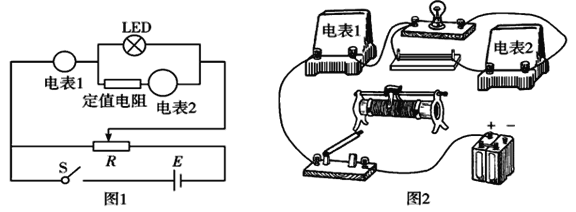
��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������ϵxOy�ĵ�һ�����У�������ֱ���µ���ǿ�糡���糡ǿ�ȴ�СΪ4E0�������ǵ糡������߽��ߣ������Ҷ���x��Ľ���ΪA��A������Ϊ��L��0��������x����Χ�ɵĿռ���û�е糡���ڵڶ�������ˮƽ���ҵ���ǿ�糡���糡ǿ�ȴ�СΪE0��M����L��L����N����L��0���������������һ���������ӵķ�����װ�ã�����������Ϊm���������Ϊq��ֹ�Ĵ���������ӣ��������ӵ�����������֮�������ã�������װ�ô�������У�
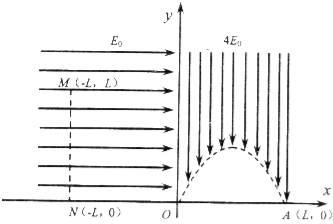
��1�������Ӵ�M���ɾ�ֹ��ʼ�˶��������һ����ʼ���ڵ糡���˶���ǡ�õ���A�㣬����������и������˶���ʱ�估����A����ٶȴ�С��
��2������MN����M���·��ɾ�ֹ�������������ӣ��ڵڶ����ĵ糡���ٺ���һ���ĵ糡ƫת�������߽߱���ܵ���A�㣬��˱߽磨ͼ�����ߣ����̣�
���𰸡���1��![]() ��
��![]() ��2��
��2��![]() ����
����![]()
��������
���������ڵڶ����ĵ糡���ȼ��ٵ�ʱ�䣺![]()
��ʱ�䣺![]() ����y����ٶȣ�
����y����ٶȣ�![]()
�ڵ�һ��������ƽ���˶���ˮƽ��![]() ���ã�
���ã�![]()
��ֱ��![]()
��������и��������õ�ʱ�䣺![]()
�ù��������ӵ���A����ٶȣ�![]()
��2�������Ӵ�P������Ϊ��-L��y0���ɾ�ֹ�ȼ���ֱ���˶������ӽ����һ��������ƽ���˶�����Q���������ֱ���˶�����Q������Ϊ��x��y�������ӽ����һ�����ٶȣ�![]()
����ƽ���˶���Q��ʱ��ˮƽ��![]()
��ֱ��![]()
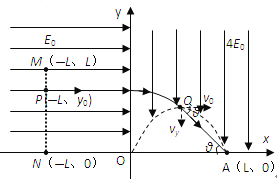
����ã�![]()
��������ʽ����ã�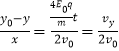
QA��x���![]() �ǿɵã�
�ǿɵã�![]() ��
��
���ٶȷֽ⣺![]() ��
��
�����ñ߽緽�̣�![]() ����
����![]()