题目内容
如图所示，质量为m的物块与转台之间能出现的最大静摩擦力为物体重力的k倍，它与转轴OO/相距R，物块随转台由静止开始转动。当转速增加到一定值时，物块即将在转台上滑动。在物块由静止到开始滑动前的这一过程中，转台对物块做的功为
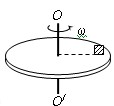
| A．0 | B．2πkmgR |
| C．2kmgR | D．kmgR/2 |
D
分析：通过题目情境我们发现在物块由静止到开始滑动前的这一过程中，转台对物块的作用力是一个变力，
对于变力做的功我们应该首先想到运用动能定理．
对于圆周运动的临界问题，我们要通过临界条件列出等式．
解答：解：由于物体做圆周运动，物体刚开始滑动这一时刻，物体受到转台的摩擦力达到最大静摩擦力去提供向心力．
即：kmg=m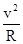
，v2=kgR．
设转台对物块做的功为W转，运用动能定理研究在物块由静止到开始滑动前的这一过程，
W转=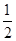
mv2-0=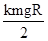
故选D．
对于变力做的功我们应该首先想到运用动能定理．
对于圆周运动的临界问题，我们要通过临界条件列出等式．
解答：解：由于物体做圆周运动，物体刚开始滑动这一时刻，物体受到转台的摩擦力达到最大静摩擦力去提供向心力．
即：kmg=m
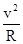，v2=kgR．设转台对物块做的功为W转，运用动能定理研究在物块由静止到开始滑动前的这一过程，
W转=
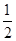mv2-0=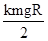故选D．
练习册系列答案
相关题目
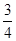倍，要使车能安全沿桥面行驶，求在此处车的速度应在什么范围内？
的仰角斜向上方抛出，初速度为v0，则石块落地时的速率与下列哪些物理量有关: ( )