题目内容
7.物体以某一初速度冲上一光滑斜面,前4s的位移为1.6m,随后4s的位移为零(物体做匀变速运动),求:(1)加速度大小为多少?
(2)物体的初速度大小为多少?
(3)第二个4秒内的速度变化量?
分析 (1)物体后4s的位移是0,可推出物体先用两秒的时间速度减到0,再用两秒反方向匀加速回去,所以物体上升过程总共花了6s,即物体向上做匀减速直线运动6s末减为零;我们可以用其逆过程来解决此问题,相当于物体从最高点做初速度为零的匀加速直线运动,结合匀变速直线运动的位移时间关系式解出此题
(2)根据速度时间公式求的初速度;
(3)根据速度时间公式求的速度变化量
解答 解:(1)我们用逆过程来解决此问题,相当于物体从最高点A做初速度为零的匀加速直线运动,BC间距为1.6m所用时间
t2=4s,AB间的时间间隔为t1=2s,
由位移时间关系式:xAB=$\frac{1}{2}$at12
xAC=$\frac{1}{2}$a(t1+t2)2
由于xAC-xAB=1.6m
把①②代入③解得:a=0.1m/s2
(2)初速度为v0=a(t1+t2)=0.1×6m/s=0.6m/s
(3)4s末速度根据v=v0+at 可求得v4=0.2m/s
8s末速度为v8=-0.2m/s 则△v=v8-v4=-0.4m/s
答:(1)加速度大小为=0.1m/s2
(2)物体的初速度大小为0.6m/s
(3)第二个4秒内的速度变化量为-0.4m/s
点评 注意当有些匀减速直线运动过程处理问题不方便时,可以应用其逆过程,相当于物体从最高点做初速度为零的匀加速直线运动,结合匀变速直线运动规律解题

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
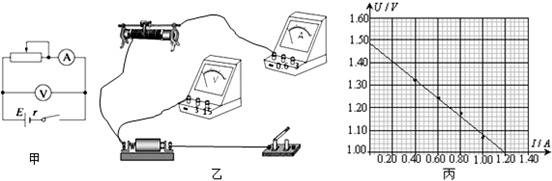
17.竖直升空的火箭,其速度-时间图象如图所示,由图可知以下说法正确的是( )


| A. | 火箭在40s时速度方向发生变化 | B. | 火箭经过40s到达最高点 | ||
| C. | 火箭经过120s落回地面 | D. | 火箭上升的最大高度为48000m |
2.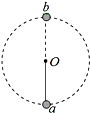 如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
 如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )
如图所示,细杆的一端与小球相连,可绕过O点的水平轴自由转动,细杆长0.5m,小球质量为3.0kg.现给小球一初速度使它做圆周运动,若小球通过轨道最低点a处的速度为va=6m/s,通过轨道最高点b处的速度为vb=2m/s,取g=10m/s2,则小球通过最低点和最高点时对细杆作用力的情况是( )| A. | a处为拉力,方向竖直向下,大小为246N | |
| B. | a处为拉力,方向竖直向上,大小为246N | |
| C. | b处为拉力,方向竖直向下,大小为6N | |
| D. | b处为压力,方向竖直向下,大小为6N |
19.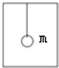 如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
 如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )
如图所示,升降机内质量为m的小球用轻绳系住,悬在升降机内,当升降机以a=$\frac{2}{3}$g减速上升时,悬绳的拉力为( )| A. | $\frac{2mg}{3}$ | B. | $\frac{mg}{3}$ | C. | $\frac{4mg}{3}$ | D. | mg |
1. 某同学学习了天体运动的知识后,假想宇宙中存在着由四颗星组成的孤立星系.一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F,母星与任意一颗小星间的万有引力为9F,则不正确的是( )
某同学学习了天体运动的知识后,假想宇宙中存在着由四颗星组成的孤立星系.一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F,母星与任意一颗小星间的万有引力为9F,则不正确的是( )
 某同学学习了天体运动的知识后,假想宇宙中存在着由四颗星组成的孤立星系.一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F,母星与任意一颗小星间的万有引力为9F,则不正确的是( )
某同学学习了天体运动的知识后,假想宇宙中存在着由四颗星组成的孤立星系.一颗母星处在正三角形的中心,三角形的顶点各有一颗质量相等的小星围绕母星做圆周运动.如果两颗小星间的万有引力为F,母星与任意一颗小星间的万有引力为9F,则不正确的是( )| A. | 每颗小星受到3个万有引力作用 | |
| B. | 每颗小星受到的万有引力为($\frac{\sqrt{3}}{2}$+9)F | |
| C. | 母星的质量是每颗小星质量的3倍 | |
| D. | 小星围绕母星做圆周运动的方向相同,周期、角速度、线速度的大小相等 |
 2014年8月20日,日本广岛县发生特大泥石流灾害.一汽车停在距离小山坡底20m处,在距坡底80m的山坡处泥石流从静止以0.4m/s2的加速度匀加速倾泻而下,当泥石流滑到坡底时,司机才突然发现并启动汽车,假设司机(反应时间为1s)以2m/s2的加速度匀加速启动汽车且一直做匀加速直线运动(如图所示),而泥石流到达坡底后速率不变且在水平面的运动近似看成匀速直线运动.问:汽车司机能否安全脱离?
2014年8月20日,日本广岛县发生特大泥石流灾害.一汽车停在距离小山坡底20m处,在距坡底80m的山坡处泥石流从静止以0.4m/s2的加速度匀加速倾泻而下,当泥石流滑到坡底时,司机才突然发现并启动汽车,假设司机(反应时间为1s)以2m/s2的加速度匀加速启动汽车且一直做匀加速直线运动(如图所示),而泥石流到达坡底后速率不变且在水平面的运动近似看成匀速直线运动.问:汽车司机能否安全脱离? 在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使一小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)
在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽轨道的末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面上,使一小球从斜槽上紧靠挡板处由静止释放,小球撞到木板并在白纸上留下痕迹A;将木板向远离槽口平移距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞在木板上得到痕迹B;又将木板再向远离槽口平移距离x,小球再从斜槽上紧靠挡板处由静止释放,再得到痕迹C.若测得木板每次移动距离x=10.00cm,A、B间距离y1=5.02cm,B、C间距离y2=14.82cm.请回答以下问题(g=9.80m/s2)