题目内容
10.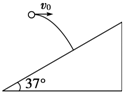 小球以15m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.取g=10m/s2,tan 53°=$\frac{4}{3}$,求:
小球以15m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.取g=10m/s2,tan 53°=$\frac{4}{3}$,求:(1)小球在空中的飞行时间;
(2)抛出点距落点的高度.
分析 (1)小球垂直撞在斜面上,速度与斜面垂直,将该速度进行分解,根据水平分速度和角度关系求出竖直分速度,再根据vy=gt求出小球在空中的飞行时间.
(2)根据h=$\frac{1}{2}g{t}^{2}$,求出抛出点距落点的高度.
解答 解:(1)将球垂直撞在斜面上的速度分解,如图所示,由图可知θ=37°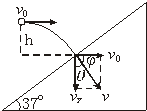
则tanθ=$\frac{{v}_{0}}{{v}_{y}}$
又vy=gt
则t=$\frac{{v}_{0}}{gtanθ}$=$\frac{15}{10×tan37°}$s=2s
故小球在空中运动的时间为2s.
(2)抛出点距落点的高度 h=$\frac{1}{2}$gt2=$\frac{1}{2}$×10×22=20m
答:
(1)小球在空中的飞行时间为2s.
(2)抛出点距离落球点的高度为20m.
点评 解决本题的关键知道垂直撞在斜面上,速度与斜面垂直,将速度分解为水平方向和竖直方向,根据水平分速度可以求出竖直分速度,从而可以求出运动的时间.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1.下列说法正确的是( )
| A. | 黑体辐射电磁波的强度按波长的分布与物体的形状有关 | |
| B. | 不确定性关系告诉我们,不可能准确地知道粒子的位置 | |
| C. | 玻尔理论的假设之一是原子能量的量子化 | |
| D. | 爱因斯坦提出了光电子的能量与入射光的强弱有关,与入射光的频率无关 |
5.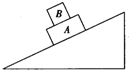 如图所示,物体B放在物体A上,A、B的上下表面均与固定粗糙斜面平行,第一种情况下,两者以某一初速度向上做匀减速运动,第二种情况下,两者从静止开始向下做匀加速运动,运动过程中A、B两者始终保持相对静止,以下说法正确的是( )
如图所示,物体B放在物体A上,A、B的上下表面均与固定粗糙斜面平行,第一种情况下,两者以某一初速度向上做匀减速运动,第二种情况下,两者从静止开始向下做匀加速运动,运动过程中A、B两者始终保持相对静止,以下说法正确的是( )
 如图所示,物体B放在物体A上,A、B的上下表面均与固定粗糙斜面平行,第一种情况下,两者以某一初速度向上做匀减速运动,第二种情况下,两者从静止开始向下做匀加速运动,运动过程中A、B两者始终保持相对静止,以下说法正确的是( )
如图所示,物体B放在物体A上,A、B的上下表面均与固定粗糙斜面平行,第一种情况下,两者以某一初速度向上做匀减速运动,第二种情况下,两者从静止开始向下做匀加速运动,运动过程中A、B两者始终保持相对静止,以下说法正确的是( )| A. | 第一种情况下B受到的摩擦力方向沿斜面向下,第二种情况下B受到的摩擦力方向沿斜面向上 | |
| B. | 第一种情况下B受到的摩擦力方向沿斜面向上,第二种情况下B受到的摩擦力方向沿斜面向下 | |
| C. | 两种情况下B受到的摩擦力均为零 | |
| D. | B受到的摩擦力情况取决于A、B表面的性质 |
15.北京时间2006年7月12日凌晨,中国“飞人”刘翔在瑞士洛桑田径超级大奖赛男子110米栏的比赛中,以12秒88打破了世界纪录!刘翔在比赛中的平均速度约为( )
| A. | 7.00m/s | B. | 7.76m/s | C. | 8.54m/s | D. | 10.00m/s |
2.下列说法中正确的是( )
| A. | 物体在恒力作用下不可能作曲线运动 | |
| B. | 物体在恒力作用下有可能作曲线运动 | |
| C. | 物体在变力作用下不可能作直线运动 | |
| D. | 物体在变力作用下有可能作直线运动 |
11.有一静电场,其电势在x方向变化的图线如图所示,则下列说法正确的是( )
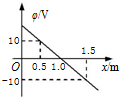

| A. | 该电场的电场强度沿x方向 | |
| B. | x=1.0m处电场强度不一定等于零 | |
| C. | 该电场的电场强度为20V/m | |
| D. | x=0.5m与1.5m两处电场强度等大、反向 |
12.线圈在匀强磁场中匀速转动,产生的交变电流如图,则( )
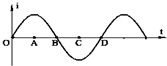

| A. | 在A和C时刻线圈平面和磁场垂直 | |
| B. | 在A和C时刻线圈磁通量变化率为零 | |
| C. | 在B时刻线圈中的磁通量为零 | |
| D. | 若线圈转动的周期为0.02s,则该交变电流的频率为50Hz |