题目内容
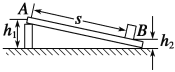
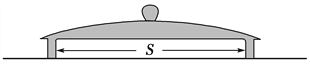
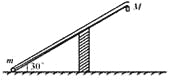
【题目】如图所示，长为L、内壁光滑的直管与水平地面成30°角固定放置。将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M=km的小物块相连，小物块悬挂于管口。现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变。(重力加速度为g)
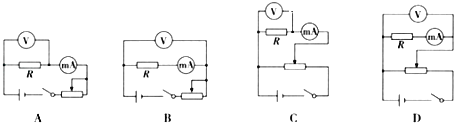
(1)求小球从管口抛出时的速度大小；
(2)试证明小球平抛运动的水平位移总小于
【答案】（1）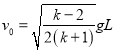
（k＞2）（2）见解析；
【解析】试题分析：（1）设M落地时的速度大小为v，m射出管口时速度大小为v0，M落地后m的加速度为a0．
根据牛顿第二定律有：-mgsin30°=ma0
对于m匀加速直线运动有：v2=2aLsin30°
对于小物块落地静止不动，小球m继续向上做匀减速运动有：v2-v02=2a0L（1-sin30°）
解得：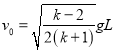 
（k＞2）
（3）平抛运动x=v0t Lsin30°=
gt2
解得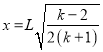
因为
＜1，所以x＜
，得证．
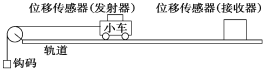
【题目】某同学设计了一个“探究加速度与力、质量关系”的实验。如图甲为实验装置图，A为小车，B为打点计时器，C为装有砂子的砂桶，D为一端带有定滑轮的长方形木板，实验中可认为细绳对小车拉力F等于砂和砂桶总重量。
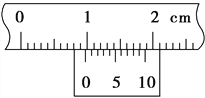
(1)图乙为某次实验得到的纸带，图中的点为实际打出来的点，已知所用交流电的频率为50Hz，则小车加速度为________m/s2(结果保留2位有效数字)。
(2)保持砂和砂桶质量不变，改变小车质量m，得到如下数据：
次数 | 1 | 2 | 3 | 4 | 5 |
小车加速度a/m·s－2 | 1.98 | 1.48 | 1.00 | 0.67 | 0.50 |
小车质量m/kg | 0.25 | 0.33 | 0.50 | 0.75 | 1.00 |
| 4.00 | 3.00 | 2.00 | 1.33 | 1.00 |
请在图丙中选择恰当物理量建立坐标系，并作出图线_______。由图线得到的结论：________。
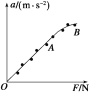
(3)保持小车质量不变，改变砂子重量，该同学根据实验数据作出了加速度a与拉力F的图线如图丁，发现该图线不通过原点，其主要原因是：______________________________。
