Question

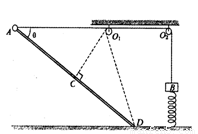
如图所示，质量m_B＝3.5kg的物体B通过一轻弹簧固连在地面上，弹簧的劲度系数k=100N/m．一轻绳一端与物体B连接，绕过无摩擦的两个轻质小定滑轮O₁、O₂后，另一端与套在光滑直杆顶端的、质量m_A＝1.6kg的小球A连接．已知直杆固定，杆长L为0.8m，且与水平面的夹角θ=37°．初始时使小球A静止不动，与A端相连的绳子保持水平，此时绳子中的张力F为45N． 已知A O₁=0.5m，绳子不可伸长．现将小球A从静止释放（重力加速度g取10m/s²，sin37°=0.6，cos37°=0.8）。求：

1.在释放小球A前弹簧的形变量；

2.若直线C O₁与杆垂直，求物体A运动到C点的过程中绳子拉力对物体A所做的功；

3.求小球A运动到底端D点时的速度．

 

Answer 1

 

1.0.1cm

2.7J

3.

解析:（1）释放小球A前，物体B处于平衡状态： 得       

故弹簧被拉长了0.1cm

（2）小球从杆顶端运动到C点的过程，由动能定理：

      而

物体B下降的高度                             

由此可知，此时弹簧被压缩了0.1m，则弹簧的弹性势能在初、末状态相同。

再以A、B和弹簧为系统，由机械能守恒：                                     

对小球进行速度分解可知，小球运动到C点时物体B的速度      

由以上几式联立可得：

（3）因杆长L=0.8m，故

故DO₁=AO₁，弹簧的伸长量依然为0.1m.，与最初状态相比，弹簧的弹性势能相同，物体B又回到了初始位置，其重力势能也与最初状态相同。

在D点对A的速度进行分解可得： 

由机械能守恒：                                               

联立可得小球A运动到杆的底端D点时的速度：