Question

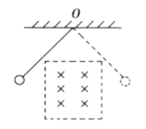
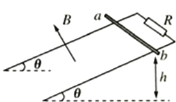
【题目】如图，一足够长的光滑平行金属轨道，其轨道平面与水平面成θ角，上端用一电阻R相连，处于方向垂直轨道平面向上的匀强磁场中，质量为m、电阻为r的金属杆ab，从高为h处由静止释放，下滑一段时间后，金属杆开始以速度v匀速运动直到轨道的底端。金属杆始终保持与导轨垂直且接触良好，轨道电阻及空气阻力均可忽略不计，重力加速度为g。则（ ）

A.金属杆加速运动过程中的平均速度小于

B.金属杆加速运动过程中克服安培力做功的功率大于匀速运动过程中克服安培力做功的功率

C.当金属杆的速度为时，它的加速度大小为

D.整个运动过程中电阻R产生的焦耳热为

Answer 1

【答案】D

【解析】

考查导体棒切割磁感线的问题。

A．加速过程中，有：

而安培力有：

电流：

电动势：

联立解得：

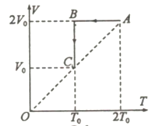
可知，加速时，速度越大，安培力越大，加速度越小，做加速度减小的减速运动，v-t图像如图：

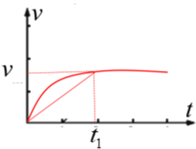
0-t1时间内，曲线为本运动的v-t图像，直线为匀加速直线运动的v-t图像，由匀加速直线运动规律可知，匀加速直线运动的平均速度为：

由图可知，相同时间内本运动位移大于匀加速直线运动的位移，所以，平均速度大于，A错误；

B．由功率公式：

可知，加速过程时，安培力小于匀速过程，平均速度也小于匀速过程，所以克服安培力做功的功率小于匀速过程，B错误；

C．当金属杆的速度为时，加速度为零：

解得：

当金属杆的速度为时，有：

联立解得：

C错误；

D．整个运动过程中整个电路产生的焦耳热为：

电阻R产生的焦耳热与总焦耳热之间的关系：

所以电阻R产生的焦耳热为：

D正确。

故选D。