Question

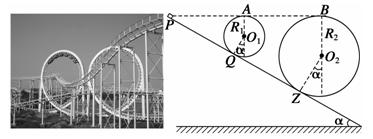
（20分）如图右图所示是游乐场中过山车的实物图片，左图所示是过山车的简化模型图。在模型图中水平倾角都为α＝37°，斜轨道AB、CD、EF与竖直光滑圆形（圆弧）轨道圆滑连接。B、C、D、E、F为对应的切点。其中两个圆轨道半径分别为R₁＝6.0m和R₃＝3.0m，中间圆弧轨道的半径为R₂。且两圆形轨道的最高点P、Q与A、D、E点平齐。现使小车（视作质点）从A点以一定的初速度沿斜面向下运动。已知斜轨道面与小车间的动摩擦因数为μ＝1/24，g＝10m/s²，sin37º＝0.6，cos37º＝0.8，tan18.5⁰=1/3。问：

⑴若小车恰好能通过第一个圆形轨道的最高点P处，则其在A点的初速度应为多大？

⑵若在⑴问情况下小车能安全到达Ｅ点，则能否安全通过第三个圆形轨道的Q点？

⑶若小车在A点的初速度为m/s，且R₂=10m则小车能否安全通过整段轨道？

 

 

Answer 1

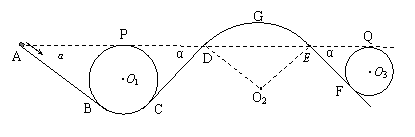
解析：（1）小车恰好过P点，故有

          

得 　　  　（1）

   小车由A到P的过程，由动能定理有

           　　　  （２）

由几何关系可得

                 （3）

由（1）（2）（3）并代入数据得

            　  　（4）

（2）设小车能够通过Q点，则A到Q由动能定理得

  （5）

其中 

代入数据可得

         （6）

而车恰好能过Ｑ点时，在Ｑ点的速度为      （7）

故小车能安全通过第三圆轨道       （8）

（3）小车以v=m/s的初速度从P点下滑时，因为有

所以，小车可以通过第一圆形轨道        （9）

设小车到中间圆弧最高点G的速度为，则A到Ｇ由动能定理得

       （10）

其中 

代入数据可得      （11）

小车在最高点要不脱离轨道必须满足

所以小车在中间轨道上有脱离轨道的危险。即小车不能安全通过整段轨道。     （12）

评分标准：共20分，其中(4)(6)(9)(11)每式1分，其余每式2分。