题目内容
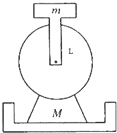 在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求
在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求
(1)m运动至什么位置时打夯机对地面的压力最大?
(2)电动机的最小角速度.
解:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)当铁块运动到最高点时,打夯机才会离开地面,受到地面的支持力为零,此时设杆的拉力为F,则由牛顿第二定律:
对M有:F-Mg=0
对m有:mg+F=mlω2
解得:ω=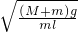
答:(1)m运动至最低点位置时打夯机对地面的压力最大;
(2)电动机的最小角速度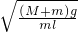 .
.
分析:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)电动机的角速度最小时,连杆转动到最高点时,对地压力恰好为零.
点评:本题取材于生产实践中的一个具体实例,解题的关键采用隔离法分析,对铁块,在竖直方向上的合力提供圆周运动的向心力.对打夯机受力平衡.
(2)当铁块运动到最高点时,打夯机才会离开地面,受到地面的支持力为零,此时设杆的拉力为F,则由牛顿第二定律:
对M有:F-Mg=0
对m有:mg+F=mlω2
解得:ω=
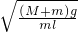
答:(1)m运动至最低点位置时打夯机对地面的压力最大;
(2)电动机的最小角速度
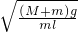 .
.分析:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)电动机的角速度最小时,连杆转动到最高点时,对地压力恰好为零.
点评:本题取材于生产实践中的一个具体实例,解题的关键采用隔离法分析,对铁块,在竖直方向上的合力提供圆周运动的向心力.对打夯机受力平衡.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
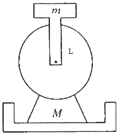 (2008?增城市模拟)在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求
(2008?增城市模拟)在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求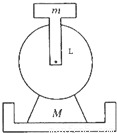
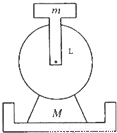
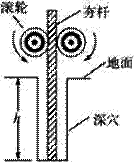 建筑工地有一种“深坑打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转动可将夯杆从深为h=6.4m的坑中提上来。当夯杆底端升至坑口时,夯杆被释放,最后夯杆在自身重力作用下,落回深坑,夯实坑底。之后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滑轮边缘的线速度v恒为4m/s,每个滚轮对夯杆的正压力F=2×104N,滚轮与夯杆间的动摩擦因素µ=0.3,夯杆质量m=1×103kg,坑深h=6.4m。假定在打夯过程中坑的深度变化不大,.取g=10m/s2,求:
建筑工地有一种“深坑打夯机”。工作时,电动机带动两个紧压夯杆的滚轮匀速转动可将夯杆从深为h=6.4m的坑中提上来。当夯杆底端升至坑口时,夯杆被释放,最后夯杆在自身重力作用下,落回深坑,夯实坑底。之后,两个滚轮再次压紧,夯杆再次被提上来,如此周而复始工作。已知两个滑轮边缘的线速度v恒为4m/s,每个滚轮对夯杆的正压力F=2×104N,滚轮与夯杆间的动摩擦因素µ=0.3,夯杆质量m=1×103kg,坑深h=6.4m。假定在打夯过程中坑的深度变化不大,.取g=10m/s2,求: 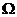 的定值电阻
的定值电阻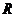 .在水平虚线
.在水平虚线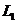 、
、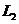 间有一与导轨所在平面垂直的匀强磁场
间有一与导轨所在平面垂直的匀强磁场 、磁场区域的高度为
、磁场区域的高度为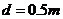 .导体棒
.导体棒 的质量
的质量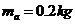 ,电阻
,电阻
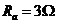 ;导体棒
;导体棒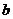 的质量
的质量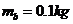 ,电阻
,电阻 .它们分别从图中
.它们分别从图中 、
、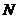 处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当
处同时由静止开始在导轨上无摩擦向下滑动,且都能匀速穿过磁场区域,当