题目内容
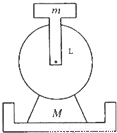
在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求(1)m运动至什么位置时打夯机对地面的压力最大?
(2)电动机的最小角速度.
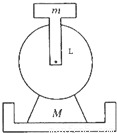
【答案】分析:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)电动机的角速度最小时,连杆转动到最高点时,对地压力恰好为零.
解答:解:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)当铁块运动到最高点时,打夯机才会离开地面,受到地面的支持力为零,此时设杆的拉力为F,则由牛顿第二定律:
对M有:F-Mg=0
对m有:mg+F=mlω2
解得:ω=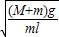
答:(1)m运动至最低点位置时打夯机对地面的压力最大;
(2)电动机的最小角速度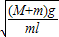 .
.
点评:本题取材于生产实践中的一个具体实例,解题的关键采用隔离法分析,对铁块,在竖直方向上的合力提供圆周运动的向心力.对打夯机受力平衡.
(2)电动机的角速度最小时,连杆转动到最高点时,对地压力恰好为零.
解答:解:(1)当铁块运动到最低点时打夯机对地面的压力最大.
(2)当铁块运动到最高点时,打夯机才会离开地面,受到地面的支持力为零,此时设杆的拉力为F,则由牛顿第二定律:
对M有:F-Mg=0
对m有:mg+F=mlω2
解得:ω=
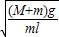
答:(1)m运动至最低点位置时打夯机对地面的压力最大;
(2)电动机的最小角速度
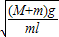 .
.点评:本题取材于生产实践中的一个具体实例,解题的关键采用隔离法分析,对铁块,在竖直方向上的合力提供圆周运动的向心力.对打夯机受力平衡.

练习册系列答案
相关题目
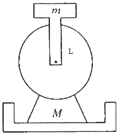 (2008?增城市模拟)在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求
(2008?增城市模拟)在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求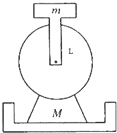 在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求
在建筑工地上有一种打夯机,其结构原理如图所示,用一长为L的连杆(质量可忽略)一端固定一质量为m的铁块,另一端固定在电动机的转轴上.铁块m可在竖直平面内做圆周运动,当旋转的角速度达到一定的数值,可使质量为M(不包括铁块质量m)的打夯机离开地面,然后砸向地面,从而起到夯实地基的作用.求