题目内容
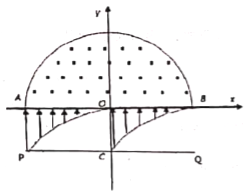
【题目】如图,在坐标平面内,第三、四象限内一R<x<R的范围内有y方向的匀强电场(临界虚线PO上有电场、但临界虚线CB上无电场)。电场强度为E,电场的下边界方程分别为![]() (-R≤x<0),
(-R≤x<0),![]() (0≤x<R),电荷可以自由穿越边界,在一、二象限内有垂直于纸面向外,边界方程为x2+y2=R2的匀强磁场;在y=-R/2处有一荧光屏,荧光屏PQ长度为2R,中点C在y轴上,在第三象限中电场的下边界上,均匀分布着粒子发射源,不断由静止发出许多质量为m,电量为q的正粒子,不计重力和粒子间相互作用力,粒子打在荧光屏上会发光。求:
(0≤x<R),电荷可以自由穿越边界,在一、二象限内有垂直于纸面向外,边界方程为x2+y2=R2的匀强磁场;在y=-R/2处有一荧光屏,荧光屏PQ长度为2R,中点C在y轴上,在第三象限中电场的下边界上,均匀分布着粒子发射源,不断由静止发出许多质量为m,电量为q的正粒子,不计重力和粒子间相互作用力,粒子打在荧光屏上会发光。求:
(1)求粒子运动半径r与释放位置的x坐标的绝对值和磁感应强度B三者之间的关系;
(2)改变磁场的磁感应强度的大小,发现屏幕上荧光只有一个亮点,请问此亮点在哪?此时磁感应强度的大小为多少?
(3)继续调整磁感应强度的大小,发现荧光屏上CO段距C点R/3至R之间有光点,求此时磁场的磁感应强度。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)对粒子在电场中的运动过程运用动能定理,粒子在磁场中的运动运用洛伦兹力提供向心力,联立即可求出粒子运动半径r与释放位置的x坐标和磁感应强度B三者之间的关系式;
(2)改变磁感应强度的大小,使屏幕上荧光只有C点一个亮点,利用(1)中结果结合几何关系,即可求出此时磁感应强度的大小;
(3)调整磁感应强度的大小,使荧光屏上CQ段且距C点R/3至R之间有光点,利用(1)中结果结合几何关系,即可求出此时磁场的磁感应强度。
(1)从第三象限电场边界处释放的粒子,由动能定理有:qE![]() x2=
x2=![]() mv2
mv2
进入磁场的速度:![]()
在磁场中粒子做匀速圆周运动,根据洛伦兹力提供向心力可得:![]()
所以半径:![]() ①
①
(2)当所有的粒子打到0点时,为荧光的左边界,根据几何关系可得:r=![]() x
x
代入①得:![]()
(3)当荧光左边界到C点R/3时,粒子来源于三象限x=-![]() 的粒子;
的粒子;
根据几何关系可得此时在磁场中的半径:![]()
代入①得:![]()

 新课标同步训练系列答案
新课标同步训练系列答案【题目】某同学用伏安法测一节干电池的电动势和内阻,现备有下列器材:
A.被测干电池一节 |
B.电流表:量程0~0.6A,内阻0.1Ω |
C.电流表:量程0~3A,内阻0.024Ω |
D.电压表:量程0~3V,内阻未知 |
E.电压表:量程0~15V,内阻未知
F.滑动变阻器:0~10Ω,2A
G.滑动变阻器:0~100Ω,1A
H.开关、导线若干
在伏安法测电池电动势和内阻的实验中,由于电流表和电压表内阻的影响,测量结果存在系统误差.在现有器材的条件下,要尽可能准确地测量电池的电动势和内阻.
(1)在上述器材中请选择适当的器材:____ ____(填写选项前的字母);
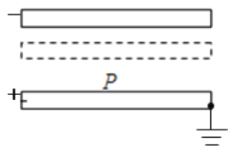
(2)在图方框中画出相应的实验电路图;

(3)根据实验中电流表和电压表的示数得到了如图所示的U-I图象,则在修正了实验系统误差后,干电池的电动势E=________V,内电阻r=________Ω.