题目内容
20.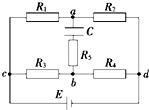 如图所示电路中,电源电动势E=10V,内电阻不计,电阻R1=14Ω,R2=6Ω,R3=2Ω,R4=8Ω,R5=10Ω,电容器的电容C=2 μF.求:
如图所示电路中,电源电动势E=10V,内电阻不计,电阻R1=14Ω,R2=6Ω,R3=2Ω,R4=8Ω,R5=10Ω,电容器的电容C=2 μF.求:(1)通过电源的电流为多少?
(2)电容器所带的电量?
(3)若R1突然断路,将有多少电荷通过R5?
分析 (1、2)当电路稳定时,R1与R2串联,R3与R4串联,两条支路并联.R5上没有电流流过.根据欧姆定律求出通过电源的电流,根据闭合电路欧姆定律求出电容器的电压,再求电量.
(3)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压,根据电容器上电压的变化判断电容器充电或放电,分析通过R5的电荷.
解答 解:(1)当电路稳定时,R1与R2串联,R3与R4串联,两条支路并联.R5上没有电流流过,
外电路总电阻为:R=$\frac{({R}_{1}+{R}_{2})({R}_{3}+{R}_{4})}{{R}_{1}+{R}_{2}+{R}_{3}+{R}_{4}}=\frac{20×10}{20+10}=\frac{20}{3}Ω$
则通过电源的电流为:I=$\frac{E}{R}=\frac{10}{\frac{20}{3}}=1.5A$
(2)设Ud=0,电容器两板间的电压即为a、b两点间的电势差.
则a点电势为:Ua=Ud+$\frac{E{R}_{2}}{{R}_{1}+{R}_{2}}$=0+$\frac{10×6}{14+6}$V=3 V.
电流由b点经R4流到d点,则b点电势为:Ub=Ud+$\frac{E{R}_{4}}{{R}_{3}+{R}_{4}}$=0+$\frac{10×8}{2+8}$V=8 V,
由Ub>Ua可知,电容器下板带正电.
b、a两点间的电势差为:Uba=Ub-Ua=5.0 V,
电容器所带的电量为:Q=CUba=1.0×10-5C.
(3)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压.此时电容器所带电量为:
Q′=CU4=C×$\frac{E{R}_{4}}{{R}_{3}+{R}_{4}}$=2×10-6×$\frac{10×8}{2+8}$C=1.6×10-5 C.
由Ub>Ud可知,电容器下板仍带正电.
由Q′>Q知,R1断路后电容器经历了一次再充电过程,电容器极板上增加的电量为:
△Q=Q′-Q=(1.6×10-5-1.0×10-5) C=6.0×10-6 C.
答:(1)通过电源的电流为1.5A;
(2)电容器所带的电量为1.0×10-5C;
(3)若R1突然断路,将有6.0×10-6 C电荷通过R5.
点评 本题是电路桥式电路,对于电容器,关键求电压.本题电路稳定时,电容器的电压等于电容器这一路同侧两个电阻的电压之差.

| A. | 该电场在某点对试探电荷的作用力大小跟试探电荷的电荷量和电性无关 | |
| B. | 以Q为球心的球面是等势面 | |
| C. | 以Q为球心的球面上各点电场强度相同 | |
| D. | 在电场中某点由静止释放一个电荷(仅受电场力),该电荷在运动过程中电势能越来越小 |
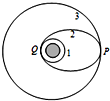 发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,其中说法正确的是( )
发射地球同步卫星要经过三个阶段:先将卫星发射至近地圆轨道1,然后使其沿椭圆轨道2运行,最后将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示.当卫星分别在1、2、3轨道上正常运行时,其中说法正确的是( )| A. | 卫星在轨道2上经过Q点时的加速度等于它在轨道1 上经过Q点时的加速度 | |
| B. | 卫星在轨道3上的动能大于它在轨道1上的动能 | |
| C. | 卫星在轨道3上的引力势能小于它在轨道1上的引力势能 | |
| D. | 卫星在轨道3上的机械能等于它在轨道1上的机械能 |
| A. | 自由电子定向移动的速率为v0 | |
| B. | 自由电子定向移动的速率为v=$\frac{I}{ne}$ | |
| C. | 自由电子定向移动的速率为真空中的光速c | |
| D. | 自由电子定向移动的速率为v=$\frac{I}{neS}$ |
| A. | 研究一端固定并可绕该端转动的木杆的运动时 | |
| B. | 研究乒乓球的旋转时,可以将乒乓球看作质点 | |
| C. | 研究一体操运动员在平衡木上的运动时 | |
| D. | 研究月球绕地球运动时 |
| A. | 小船可以到达正对岸 | |
| B. | 小船渡河时间不少于50s | |
| C. | 小船以最短时间渡河时,它沿水流方向的位移大小为200m | |
| D. | 小船以最短位移渡河时,位移大小为150m |
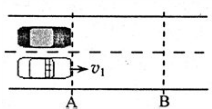 如图所示,在两车道的公路上有黑白两辆车,黑色车辆停在A线位置,某时刻白色车速度以v1=40m/s通过A线后立即以大小a1=4m/s2的加速度开始制动减速,黑车4s后开始以a2=4m/s2的加速度开始向同一方向匀加速运动,经过一定时间,两车同时
如图所示,在两车道的公路上有黑白两辆车,黑色车辆停在A线位置,某时刻白色车速度以v1=40m/s通过A线后立即以大小a1=4m/s2的加速度开始制动减速,黑车4s后开始以a2=4m/s2的加速度开始向同一方向匀加速运动,经过一定时间,两车同时