题目内容
12.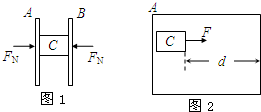 两块固定的竖直平行板A、B间夹着一块长方体木块C,C的质量为m=1kg,A、B对C的压力大小均为FN=100N.如图1所示.C距板右侧边缘的水平距离为d=1m.图2为从图1右侧看到的视图.现对C施一水平恒力F,将C从两板间以速度v=0.5m/s匀速拉出,C与A、B间的动摩擦因数均为μ=0.1,板A、B的竖直高度足够长,g取10m/s2,求
两块固定的竖直平行板A、B间夹着一块长方体木块C,C的质量为m=1kg,A、B对C的压力大小均为FN=100N.如图1所示.C距板右侧边缘的水平距离为d=1m.图2为从图1右侧看到的视图.现对C施一水平恒力F,将C从两板间以速度v=0.5m/s匀速拉出,C与A、B间的动摩擦因数均为μ=0.1,板A、B的竖直高度足够长,g取10m/s2,求(1)所施加恒力F的大小
(2)C从初始位置运动到A板右边缘所用时间.
分析 (1)C匀速运动,受力平衡,对C受力分析,根据平衡条件结合几何关系求解F;
(2)摩擦力f必须与C的运动方向相反,从而判断出C的运动方向,根据几何关系求出C运动的位移,从而求出运动的时间.
解答 解:(1)C匀速运动,受力平衡,对C受力分析,如图所示:
滑动摩擦力f=2μFN=20N
由勾股定理得:
F=$\sqrt{{f}^{2}-(mg)^{2}}=\sqrt{2{0}^{2}-1{0}^{2}}=10\sqrt{3}$N
(2)摩擦力f必须与C的运动方向相反,所以C的速度v的方向与水平成θ角斜向下.
根据几何关系得:
$sinθ=\frac{mg}{f}=\frac{10}{20}=\frac{1}{2}$
则θ=30°
当C从初始位置运动到A板右边缘所走过的位移为x=$\frac{d}{cosθ}$
运动时间t=$\frac{x}{v}$
解得:t=$\frac{4\sqrt{3}}{3}s$
答:(1)所施加恒力F的大小为$10\sqrt{3}N$;
(2)C从初始位置运动到A板右边缘所用时间为$\frac{4\sqrt{3}}{3}s$.
点评 本题要特别注意物体C不是沿水平方向运动的,要能根据受力情况求出速度方向,明确运动的位移不是d,难度适中.

练习册系列答案
相关题目
2.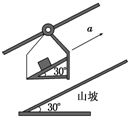 乘坐“空中缆车”饱览大自然的美景是旅游者绝妙的选择.若某一缆车沿着坡度为30°的山坡以加速度a上行,如图所示.在缆车中放一个与山坡表面平行的斜面,斜面上放一个质量为m的小物块,小物块相对斜面静止(设缆车保持竖直状态运行).则( )
乘坐“空中缆车”饱览大自然的美景是旅游者绝妙的选择.若某一缆车沿着坡度为30°的山坡以加速度a上行,如图所示.在缆车中放一个与山坡表面平行的斜面,斜面上放一个质量为m的小物块,小物块相对斜面静止(设缆车保持竖直状态运行).则( )
 乘坐“空中缆车”饱览大自然的美景是旅游者绝妙的选择.若某一缆车沿着坡度为30°的山坡以加速度a上行,如图所示.在缆车中放一个与山坡表面平行的斜面,斜面上放一个质量为m的小物块,小物块相对斜面静止(设缆车保持竖直状态运行).则( )
乘坐“空中缆车”饱览大自然的美景是旅游者绝妙的选择.若某一缆车沿着坡度为30°的山坡以加速度a上行,如图所示.在缆车中放一个与山坡表面平行的斜面,斜面上放一个质量为m的小物块,小物块相对斜面静止(设缆车保持竖直状态运行).则( )| A. | 小物块受到的摩擦力方向平行斜面向上 | |
| B. | 小物块受到的摩擦力方向平行斜面向下 | |
| C. | 小物块受到的滑动摩擦力为$\frac{1}{2}$mg+ma | |
| D. | 小物块受到的静摩擦力为ma |
7.下列几组共点力分别作用在一个物体上,有可能使物体处于平衡状态的是( )
| A. | 7 N,5 N,3 N | B. | 3 N,4 N,8 N | C. | 4 N,10 N,5 N | D. | 4 N,12 N,8 N |
17. 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )| A. | 钢索对O点的拉力变大 | |
| B. | 硬杆对O点的弹力变小 | |
| C. | 钢索和硬杆对O点的作用力的合力变大 | |
| D. | 钢索和硬杆对O点的作用力的合力变小 |
4.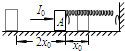 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
 如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )
如图所示,劲度系数为k的轻弹簧的一端固定在墙上,另一端与置于水平面上质量为m的物体A接触,但未与物体A连接,弹簧水平且无形变.现对物体A施加一个水平向右的瞬间冲量,大小为I0,测得物体A向右运动的最大距离为x0,之后物体A被弹簧弹回最终停在距离初始位置左侧2x0处.已知弹簧始终在弹簧弹性限度内,物体A与水平面间的动摩擦因数为μ,重力加速度为g,下列说法中正确的是( )| A. | 物体A整个运动过程,弹簧对物体A的冲量为零 | |
| B. | 物体A向右运动过程中与弹簧接触的时间一定小于物体A向左运动过程中与弹簧接触的时间 | |
| C. | 物体A向左运动的最大速度vm=2$\sqrt{ug{x}_{0}}$ | |
| D. | 物体A与弹簧作用的过程中,系统的最大弹性势能Ep=$\frac{{I}_{0}^{2}}{2m}$-2umgx0 |
1.两个半径为2.5cm的铜球,球心相距100cm,若各带10-6C的同种电荷时,相互作用的力为F1,各带10-6C的异种电荷时,相互作用的力为F2.则( )
| A. | F1=F2 | B. | F1<F2 | C. | F1>F2 | D. | 无法判断 |
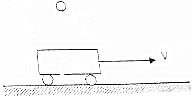 如图所示,质量为M的小车中装有细砂,正在光滑的水平面上以速度V匀速前进,这时有一个质量为m的求竖直落入车中,最后与车一起前进,求这时车的速度.
如图所示,质量为M的小车中装有细砂,正在光滑的水平面上以速度V匀速前进,这时有一个质量为m的求竖直落入车中,最后与车一起前进,求这时车的速度.