题目内容
【题目】蹦床是一项好看又惊险的运动，如图所示为运动员在蹦床运动中完成某个动作的示意图，图中虚线PQ是弹性蹦床的原始位置，A为运动员抵达的最高点，B为运动员刚抵达蹦床时的位置，C为运动员抵达的最低点，不考虑空气阻力和运动员与蹦床作用时的机械能损失，已知AB之间的高度为H，BC之间的高度为h，运动员的质量为m，重力加速度为g，取B位置的重力势能为零．求：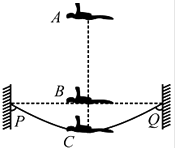
（1）运动员在A位置和C位置时的重力势能．
（2）运动员运动到B位置时的速度和运动到C位置时的弹性势能．
【答案】
（1）解：取B位置的重力势能为零，运动员在A位置和C位置时的重力势能分别为：
EPA=mgH，EPC=﹣mgh．
答：运动员在A位置和C位置时的重力势能分别为mgH和﹣mgh．
（2）解：A到B过程，根据机械能守恒定律得：mgH= 
，得 v= 
即运动员运动到B位置时的速度为 ．
由运动员和蹦床组成的系统机械能守恒得：
mgH=﹣mgh+Ep
得运动到C位置时的弹性势能 Ep=mg（H+h）
答：运动员运动到B位置时的速度为 ．运动到C位置时的弹性势能为mg（H+h）．
【解析】深刻把握理解机械能守恒定律的内涵，特别是要考虑清楚对哪个系统的哪个过程运用机械能守恒定律。
【考点精析】通过灵活运用机械能守恒及其条件，掌握在只有重力（和弹簧弹力）做功的情形下，物体动能和重力势能（及弹性势能）发生相互转化，但机械能的总量保持不变即可以解答此题．
练习册系列答案
相关题目
