题目内容
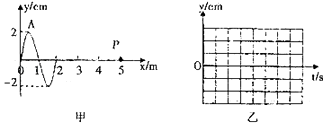
【题目】甲乙两列简谐横波在同一介质中分别沿x轴正向和负向传播，波速均为v=25cm/s，两列波在t=0时的波形曲线如图所示．求：
（i）t=0时，介质中偏离平衡位置位移为16cm的所有质点的x坐标；
（ii）从t=0开始，介质中最早出现偏离平衡位置位移为﹣16cm的质点的时间．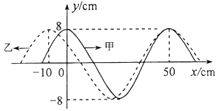
【答案】解：（i）t=0时，在x=50cm处两列波的波峰相遇，该处质点偏离平衡位置的位移为16cm，两列波的波峰相遇处的质点偏离平衡位置的位移均为16cm
从图线可以看出，甲、乙两列波的波长分别为：
λ1=50cm，λ2=60cm…①
甲、乙两列波的波峰的x坐标分别为：
x1=50+k1λ1 ， 
…②
x2=50+k2λ2 ， 
…③
③式得，介质中偏离平衡位置位移为16cm的所有质点的x坐标为：
x=（50+300n）cm n=0， 
， 
，…④
（ii）只有两列波的波谷相遇处的质点的位移为﹣16cm．t=0时，两波波谷间的x坐标之差为：
△x′=[50+（2m2+1） 
]﹣[50+（2m1+1） 
]…⑤
式中．m1和m2均为整数，将①式代入⑤式得：
△x′=10（6m2+5m1）+5
由于m1和m2均为整数，相向传播的波谷间的距离最小为：
=5cm
从t=0开始，介质中最早出现偏离平衡位置位移为﹣16cm的质点的时间为：
t= 
代入数值得：t=0.1s
答：（i）t=0时，介质中偏离平衡位置位移为16cm的所有质点的x坐标为（50+300n）cm n=0， ， ，
（ii）从t=0开始，介质中最早出现偏离平衡位置位移为﹣16cm的质点的时间为0.1s
【解析】（1）由图先读出两列波的波长和振幅，通过数学关系得知两波长的最小公倍数，对波峰相遇时的点的坐标进行分别列式，即可求出介质中偏离平衡位置位移为16cm的所有质点的x坐标．（2）先通过图表示出t=0时，两波波谷间的x坐标之差的表达式，从而可计算出相向传播的波谷间的最小距离，也就可以计算出从t=0开始，介质中最早出现偏离平衡位置位移为﹣16cm的质点的时间了．
