题目内容
 如图所示是一个竖直平面内的由倾斜直线、半径R=50cm圆弧和竖直直线三部分组成的带有凹槽的光滑轨道,且轨道的圆弧部分与倾斜部分恰好相切连接,倾斜轨道与水平面的夹角为45°.两个质量均为m=2kg的小环套在光滑轨道上,小环之间用不计质量且不可拉伸的细线相连(图中虚线表示),细线只能沿轨道的凹槽运动.开始时,让A、B两小环分别静止在圆弧轨道的最低点和倾斜轨道上,细线处于拉紧状态.释放后两小环开始运动,求:
如图所示是一个竖直平面内的由倾斜直线、半径R=50cm圆弧和竖直直线三部分组成的带有凹槽的光滑轨道,且轨道的圆弧部分与倾斜部分恰好相切连接,倾斜轨道与水平面的夹角为45°.两个质量均为m=2kg的小环套在光滑轨道上,小环之间用不计质量且不可拉伸的细线相连(图中虚线表示),细线只能沿轨道的凹槽运动.开始时,让A、B两小环分别静止在圆弧轨道的最低点和倾斜轨道上,细线处于拉紧状态.释放后两小环开始运动,求:(1)小环A运动到圆弧的最右端时的速度大小.
(2)分析小环A能否到达圆弧的最高点?如能,则计算小环到达最高点时的速度大小;如不能,则估算小环从最低点开始上升的最大高度.(精确到1cm)
分析:(1)把A、B两个小环看成一个整体,它们速度大小相等,从初位置运动到A球到达最右端的过程中运用机械能守恒即可求解速度;
(2)假设小环能上升到最高点,运用机械能守恒列式进行分析判断.若不能,由机械能守恒和几何知识求解最大高度.
(2)假设小环能上升到最高点,运用机械能守恒列式进行分析判断.若不能,由机械能守恒和几何知识求解最大高度.
解答:解:(1)对整体从初位置运动到A球到达最右端的过程中运用机械能守恒得:
×2mv2-0=-mgR+mg×
×2πR×sin45°
带入数据解得:v=0.744m/s
(2)假设小环能上升到最高点,则对整体从初位置运动到A球到达最高点的过程中运用机械能守恒得:
×2mv′2-0=-mg?2R+mg×
×2πR×sin45°
带入数据化简得:2×v′2=-2×10×1+20×0.5×
<0
故假设不可能,即说明小环A不能到达圆弧的最高点.
设小环A从最低点开始上升的最大高度为h,B沿斜面下滑的距离为S,则有
mgh=mgSsin45°
又根据数学知识有:cos
=
联立代入得:cos
=1-
解得,h≈70cm
答:(1)小环A运动到圆弧的最右端时的速度大小是0.744m/s.
(2)小环A不能到达圆弧的最高点.小环A从最低点开始上升的最大高度是70cm.
| 1 |
| 2 |
| 1 |
| 4 |
带入数据解得:v=0.744m/s
(2)假设小环能上升到最高点,则对整体从初位置运动到A球到达最高点的过程中运用机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
带入数据化简得:2×v′2=-2×10×1+20×0.5×
| ||
| 2 |
故假设不可能,即说明小环A不能到达圆弧的最高点.
设小环A从最低点开始上升的最大高度为h,B沿斜面下滑的距离为S,则有
mgh=mgSsin45°
又根据数学知识有:cos
| S |
| R |
| R-h |
| R |
联立代入得:cos
| ||
| 50 |
| h |
| 50 |
解得,h≈70cm
答:(1)小环A运动到圆弧的最右端时的速度大小是0.744m/s.
(2)小环A不能到达圆弧的最高点.小环A从最低点开始上升的最大高度是70cm.
点评:本题是系统的机械能守恒问题,环到达最高点的临界条件是速度等于零,要善于运用假设进行分析.

练习册系列答案
相关题目
 (2009?盐城模拟)如图所示,一个质量为m、带电荷量为+q的物体处于场强按E=kt规律(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与绝缘竖直墙壁间的动摩擦因数为μ,当t=0时,物体由静止释放.若最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( )
(2009?盐城模拟)如图所示,一个质量为m、带电荷量为+q的物体处于场强按E=kt规律(k为大于零的常数,取水平向左为正方向)变化的电场中,物体与绝缘竖直墙壁间的动摩擦因数为μ,当t=0时,物体由静止释放.若最大静摩擦力等于滑动摩擦力,且电场空间和墙面均足够大,下列说法正确的是( ) 如图所示,一个质量为m的带正电荷量为q的尘粒以竖直向上的初速度v0在平行板电容器P、Q两板正中间的A点进入场强为E的匀强电场中,恰好垂直于Q板打在B点,且AC=BC,则下列说法正确的是( )
如图所示,一个质量为m的带正电荷量为q的尘粒以竖直向上的初速度v0在平行板电容器P、Q两板正中间的A点进入场强为E的匀强电场中,恰好垂直于Q板打在B点,且AC=BC,则下列说法正确的是( )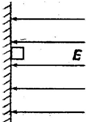 如图所示,一个质量m,带正电q的物体处于场强按E=E0__kt(E0、k均为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间的动摩擦因数为μ,当t=0时,物体处于静止状态.若电场空间和墙面均足够大,下列说法正确的是( )
如图所示,一个质量m,带正电q的物体处于场强按E=E0__kt(E0、k均为大于零的常数,取水平向左为正方向)变化的电场中,物体与竖直墙壁间的动摩擦因数为μ,当t=0时,物体处于静止状态.若电场空间和墙面均足够大,下列说法正确的是( ) 如图所示,在竖直的xOy平面上,有一根绝缘光滑的抛物线型硬杆,抛物线方程为y=kx2,其中k为正常数.空间中有沿x轴正向的匀强电场.一个套在杆上带正电的小环在轨道的A点由静止开始滑下,轨道上的B点与A点关于y轴对称.对于带电小环的下列说法,正确的是( )
如图所示,在竖直的xOy平面上,有一根绝缘光滑的抛物线型硬杆,抛物线方程为y=kx2,其中k为正常数.空间中有沿x轴正向的匀强电场.一个套在杆上带正电的小环在轨道的A点由静止开始滑下,轨道上的B点与A点关于y轴对称.对于带电小环的下列说法,正确的是( )