Question

【题目】如图所示，一个人用一根长R=1.6m的轻质细绳拴着一个质量m=1kg的小球在竖直平面内做圆周运动，已知圆心O距离地面h=4.8m，转动中小球在最低点时绳子刚好断裂，此时小球的速度12m/s，试求：（g=10m/s2）

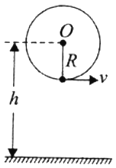
（1）小球恰好经过最高点时的速度大小；

（2）绳子能够承受的最大拉力大小；

（3）上述第（2）问中绳子断后小球的位移大小。

Answer 1

【答案】（1）小球恰好经过最高点时的速度大小是4m/s；（2）绳子能够承受的最大拉力大小是100（3）上述第（2）问中绳子断后小球的位移大小是 10.1m。

【解析】

（1）小球在竖直平面内恰好做圆周运动，在最高点的重力提供向心力，则：

代入数据可得：v=4m/s

（2）由题意，绳子被拉断前的瞬间，由牛顿第二定律有：F-mg=m

代入数据解得：F=100N；

（3）绳断后，小球做平抛运动，水平方向做匀速直线运动，竖直方向做自由落体运动，则由平抛运动的规律有：

h-R=gt2

x=vt

解得：x=v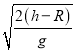

代入数据可得：x=9.6m

小球的位移：s=

代入数据可得：s=10.1m