题目内容
15.小孩喜欢玩碰碰车,设每个碰碰车的质量为m0,某次游玩时,有甲、乙两小孩驾驶碰碰车,在相距L处双方都关闭动力的情况下,以速度v沿同一直线相向而行,已知两车所受阻力均为其总重力的k倍,甲的质量为m1,乙的质量为m2,求:(当地的重力加速度为g)(1)甲、乙两人驾驶的碰碰车(含人)在碰撞前的动量大小.
(2)甲、乙两人驾驶的碰碰车经过多长时间发生碰撞.
分析 (1)甲、乙两人驾驶的碰碰车在碰撞前都在阻力作用下做匀减速直线运动,根据牛顿第二定律求出加速度,根据运动学基本公式求出位移,根据位移之和为L求出碰撞前速度,进而求出碰撞前的动量;
(2)根据$t=\frac{△v}{a}$求出甲、乙两人驾驶的碰碰车经过多长时间发生碰撞.
解答 解:(1)甲、乙两人驾驶的碰碰车在碰撞前都在阻力作用下做匀减速直线运动,根据牛顿第二定律得:
对甲有:${a}_{1}=\frac{{-k(m}_{1}+{m}_{0})g}{{m}_{1}+{m}_{0}}=-kg$,
对乙有:${a}_{2}=\frac{-k{(m}_{2}+{m}_{0})g}{{m}_{2}+{m}_{0}}=-kg$,
则甲乙两人做匀减速直线运动的加速度相同,而初速度相同,运动的时间也相等,所以相撞时,运动的位移相等,
即${x}_{1}={x}_{2}=\frac{L}{2}$,
根据匀变速直线运动位移速度公式${v}^{2}-{{v}_{0}}^{2}=2ax$可得:碰撞时的速度v1=v2=$\sqrt{{v}^{2}-kgL}$,
则碰撞前甲驾驶的碰碰车的动量${P}_{1}=({m}_{0}+{m}_{1})\sqrt{{v}^{2}-kgL}$,乙驾驶的碰碰车的动量${P}_{2}=({m}_{0}+{m}_{2})\sqrt{{v}^{2}-kgL}$
(2)设经过时间t发生碰撞,根据速度时间公式得:
t=$\frac{△v}{a}=\frac{v-\sqrt{{v}^{2}-kgL}}{kg}$
答:(1)甲、乙两人驾驶的碰碰车(含人)在碰撞前的动量大小分别为$({m}_{0}+{m}_{1})\sqrt{{v}^{2}-kgL}$和$({m}_{0}+{m}_{2})\sqrt{{v}^{2}-kgL}$.
(2)甲、乙两人驾驶的碰碰车经过时间$\frac{v-\sqrt{{v}^{2}-kgL}}{kg}$发生碰撞.
点评 本题主要考查了牛顿第二定律及运动学基本公式的直接应用,解题时抓住两车的位移之和为L且运动时间相等列式求解,难度适中.

 全程金卷系列答案
全程金卷系列答案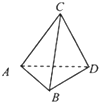 如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )
如图所示,A,B,C,D是真空中一正四面体的四个顶点,现在在A,B两点分别固定电荷量为+q,-q的两个点电荷,则关于C,D两点的磁场和电势,下列说法正确的是( )| A. | C,D两点的电场强度不同,电势相同 | |
| B. | C,D两点的电场强度相同,电势不同 | |
| C. | 将一正电荷从C点移到D点,电场力对该正电荷先做正功,然后做负功 | |
| D. | 将一正电荷从C点移到D点,电场力对该正电荷先做负功,然后做正功 |
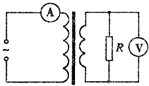 如图所示,理想变压器原、副线圈匝数之比为5:1.原线圈接入一电压为u=U0sinωt的交流电源,副线圈接一个R=22Ω的负载电阻.若U0=220$\sqrt{2}$V,ω=100πrad/s,则下述结论正确的是( )
如图所示,理想变压器原、副线圈匝数之比为5:1.原线圈接入一电压为u=U0sinωt的交流电源,副线圈接一个R=22Ω的负载电阻.若U0=220$\sqrt{2}$V,ω=100πrad/s,则下述结论正确的是( )| A. | 副线圈中电压表的示数为44V | |
| B. | 副线圈中输出交流电的周期为$\frac{1}{100π}$s | |
| C. | 原线圈中电流表的示数为2A | |
| D. | 原线圈中的输入功率为88 W |
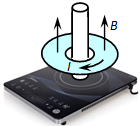 某同学在电磁炉面板上竖直放置一纸质圆筒,圆筒上套一环形轻质铝箔,电磁炉产生的交变磁场的频率、强度及铝箔厚度可以调节.现给电磁炉通电,发现铝箔悬浮了起来.若只改变其中一个变量,则( )
某同学在电磁炉面板上竖直放置一纸质圆筒,圆筒上套一环形轻质铝箔,电磁炉产生的交变磁场的频率、强度及铝箔厚度可以调节.现给电磁炉通电,发现铝箔悬浮了起来.若只改变其中一个变量,则( )| A. | 增强磁场,铝箔悬浮高度将不变 | |
| B. | 铝箔越薄,铝箔中产生的感应电流越大 | |
| C. | 增大频率,铝箔中产生的感应电流增大 | |
| D. | 在刚接通电源产生如图磁场的瞬间,铝箔中会产生如图所示的电流 |
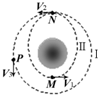 2010年10月1日下午嫦娥二号由“长征三号丙”运载火箭发射升空,经中途修正,在近月点自主实施制动,实现月球捕获,变轨后进入100公里环月圆轨道Ⅰ.在环月运行期间,卫星将择机实施轨道机动,进入100公里×15公里的椭圆轨道Ⅱ,开展技术验证和二期工程备选着陆区成像试验.(如图)M、N分别为轨道Ⅱ上的点,P为轨道Ⅰ上的点,V1、V2、V3为卫星在对应点的速度,a1、a2、a3为在对应点的加速度,则( )
2010年10月1日下午嫦娥二号由“长征三号丙”运载火箭发射升空,经中途修正,在近月点自主实施制动,实现月球捕获,变轨后进入100公里环月圆轨道Ⅰ.在环月运行期间,卫星将择机实施轨道机动,进入100公里×15公里的椭圆轨道Ⅱ,开展技术验证和二期工程备选着陆区成像试验.(如图)M、N分别为轨道Ⅱ上的点,P为轨道Ⅰ上的点,V1、V2、V3为卫星在对应点的速度,a1、a2、a3为在对应点的加速度,则( )| A. | V1>V2 | B. | V2>V3 | C. | a1>a2 | D. | a2>a3 |
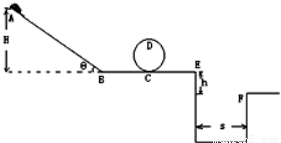
 如图所示,质量相等的两个物块A和B用跨过滑轮的轻绳相连,不计摩擦和滑轮质量,B物块套在光滑的竖直杆上,在B下落的过程中,下列说法正确的是( )
如图所示,质量相等的两个物块A和B用跨过滑轮的轻绳相连,不计摩擦和滑轮质量,B物块套在光滑的竖直杆上,在B下落的过程中,下列说法正确的是( )| A. | 物块B减少的机械能等于物块A增加的机械能 | |
| B. | 物块B减少的重力势能等于物块A和B增加的动能之和 | |
| C. | 绳拉力对A做的功等于B克服绳拉力做的功 | |
| D. | 物块A和B的速度大小相等 |
| A. | ${\;}_{13}^{27}$A+${\;}_{0}^{1}$n→${\;}_{12}^{27}$Mg+X | B. | ${\;}_{11}^{24}$Na→${\;}_{12}^{24}$Mg+X | ||
| C. | ${\;}_{4}^{9}$Be+${\;}_{2}^{4}$He→${\;}_{6}^{12}$C+X | D. | ${\;}_{92}^{239}$U→${\;}_{93}^{239}$Np+X |