题目内容
6. 某同学设计了如图所示的趣味实验来研究碰撞问题,用材料和长度相同的不可伸长的轻绳依次将N个大小相同、质量不等的小球悬挂于水平天花板下方,且相邻的小球静止时彼此接触但无相互作用力,小球编号从左到右依次为1、2、3、…、N,每个小球的质量为其相邻左边小球质量的k倍(k<1).在第N个小球右侧放置一倾角α=37°的斜面,斜面左侧靠近第N个小球处有一光滑平台,平台上放置一小球P,小球P的质量与第N个小球的质量相等,所有小球的球心等高.现将1号小球由最低点向左拉起高度h,保持绳绷紧状态由静止释放1号小球,使其与2号小球碰撞,2号小球再与3号小球碰撞….所有碰撞均为在同一直线上的正碰且无机械能损失.已知sin37°=0.6,cos37°=0.8;重力加速度为g,空气阻力、小球每次碰撞时间均可忽略不计.
某同学设计了如图所示的趣味实验来研究碰撞问题,用材料和长度相同的不可伸长的轻绳依次将N个大小相同、质量不等的小球悬挂于水平天花板下方,且相邻的小球静止时彼此接触但无相互作用力,小球编号从左到右依次为1、2、3、…、N,每个小球的质量为其相邻左边小球质量的k倍(k<1).在第N个小球右侧放置一倾角α=37°的斜面,斜面左侧靠近第N个小球处有一光滑平台,平台上放置一小球P,小球P的质量与第N个小球的质量相等,所有小球的球心等高.现将1号小球由最低点向左拉起高度h,保持绳绷紧状态由静止释放1号小球,使其与2号小球碰撞,2号小球再与3号小球碰撞….所有碰撞均为在同一直线上的正碰且无机械能损失.已知sin37°=0.6,cos37°=0.8;重力加速度为g,空气阻力、小球每次碰撞时间均可忽略不计.(1)求1号小球与2号小球碰撞之前的速度v1大小;
(2)求P小球离开光滑平台时的速度vP的大小;
(3)若N=5,且发现P小球离开平台后第一次落于斜面上与P点竖直高度差为H=$\frac{64}{9}$h的Q点,求k的值.
分析 1、对于1号小球由h高运动到最低点过程,根据机械能守恒求出碰前的速度
2、对于1、2号小球碰撞的过程根据动量守恒定律和机械能守恒列出等式,对于2、3号小球碰撞的过程,根据动量守恒定律和机械能守恒求解
3、因为5号小球与P小球质量相等,可知二者发生碰撞后交换速度,P球此后做平抛运动,根据平抛运动基本公式列式即可求解.
解答 解:(1)设1号小球的质量为m1,碰前的速度为v1,
对于1号小球由h高运动到最低点过程,根据机械能守恒
${m}_{1}gh=\frac{1}{2}{m}_{1}{{v}_{1}}^{2}$
解得:${v}_{1}=\sqrt{2gh}$
(2)设1号、2号小球碰撞后的速度分别为v1′和v2,取水平向右为正方向.
对于1、2号小球碰撞的过程,根据动量守恒定律有
m1v1=m1v'1+m2v2
根据机械能守恒有 $\frac{1}{2}{m}_{1}{{v}_{1}}^{2}=\frac{1}{2}{m}_{1}{v}_{1}{′}^{2}+\frac{1}{2}{m}_{2}{{v}_{2}}^{2}$
解得:${v}_{2}=\frac{2}{1+k}\sqrt{2gh}$
设2号、3号小球碰撞后的速度分别为v2′和v3,
对于2、3号小球碰撞的过程,根据动量守恒定律有 m2v2=m2v'2+m3v3
根据机械能守恒有 $\frac{1}{2}{m}_{2}{{v}_{2}}^{2}=\frac{1}{2}{m}_{2}{v}_{2}{′}^{2}+\frac{1}{2}{m}_{3}{{v}_{3}}^{2}$
同理可解得:3号小球被碰后的速度 ${v}_{3}=(\frac{2}{1+k})^{2}\sqrt{2gh}$
则第N个球与P碰撞前的速度${v}_{N}={(\frac{2}{1+k})}^{N-1}\sqrt{2gh}$,
而小球P的质量与第N个小球的质量相等,且发生正碰,速度交换,则P小球离开光滑平台时的速度vP=${v}_{N}={(\frac{2}{1+k})}^{N-1}\sqrt{2gh}$
(3)由(2)中的结果可推知5号小球被碰后的速度 ${v}_{5}={(\frac{2}{1+k})}^{4}\sqrt{2gh}$
因为5号小球与P小球质量相等,可知二者发生碰撞后交换速度,
所以P小球第一次被碰撞后的速度 ${v}_{P}={(\frac{2}{1+k})}^{4}\sqrt{2gh}$
P球此后做平抛运动,则有:
H=$\frac{1}{2}g{t}^{2}$
$\frac{H}{tan37°}={v}_{P}t$,
解得:$k=\sqrt{3}-1$
答:(1)1号小球与2号小球碰撞之前的速度v1大小为$\sqrt{2gh}$;
(2)求P小球离开光滑平台时的速度vP的大小为${(\frac{2}{1+k})}^{N-1}\sqrt{2gh}$;
(3)若N=5,且发现P小球离开平台后第一次落于斜面上与P点竖直高度差为H=$\frac{64}{9}$h的Q点,k的值为$\sqrt{3}-1$.
点评 本题是利用动量守恒和机械能守恒联合解决一维碰撞问题的典型例子,其中由1号球的速度归纳第n+1号球的速度是关键,而且也是难点.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案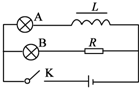 如图所示,A、B是两个完全相同的灯泡,B灯与电阻R串联,A灯与自感系数较大的线圈L串联,其直流电阻忽略不计.电源电压恒定不变,下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,B灯与电阻R串联,A灯与自感系数较大的线圈L串联,其直流电阻忽略不计.电源电压恒定不变,下列说法正确的是( )| A. | 当电键K闭合时,A比B先亮,然后A熄灭 | |
| B. | 当电键K闭合时B比A先亮,最后A比B亮 | |
| C. | 当电键K断开时,B先熄灭,A后熄灭 | |
| D. | 当电键K断开时,B先闪亮一下然后与A同时熄灭 |
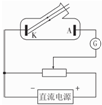 如图所示是光电管的原理图,已知当有波长为λ0的光照射到阴极K上时,电路中有光电流,则下列说法不正确的是( )
如图所示是光电管的原理图,已知当有波长为λ0的光照射到阴极K上时,电路中有光电流,则下列说法不正确的是( )| A. | 换用波长为λ1(λ1>λ0)的光照射阴极K,电路中一定没有光电流 | |
| B. | 换用波长为λ2(λ2<λ0)的光照射阴极K,电路中一定有光电流 | |
| C. | 当增大电路中电源的电压时,电路中的光电流一定增大 | |
| D. | 当将电源极性反接时,电路中一定没有光电流产生 |
| A. | m1一定大于m2 | B. | v1一定小于v2 | C. | m1一定小于m2 | D. | v1一定大于v2 |
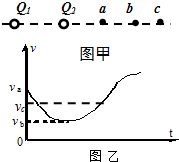 如图甲所示,Q1、Q2为两个被固定的点电荷,其中Q1带负电,a、b、c三点在它们连线的延长线上.现有一带负电的粒子以一定的初速度沿直线从a点开始向远处运动经过b、c两点(粒子只受电场力作用),粒子经过a、b、c三点时的速度分别为va、vb、vc,其速度图象如图乙所示.以下说法中错误的是( )
如图甲所示,Q1、Q2为两个被固定的点电荷,其中Q1带负电,a、b、c三点在它们连线的延长线上.现有一带负电的粒子以一定的初速度沿直线从a点开始向远处运动经过b、c两点(粒子只受电场力作用),粒子经过a、b、c三点时的速度分别为va、vb、vc,其速度图象如图乙所示.以下说法中错误的是( )| A. | Q2一定带负电 | |
| B. | Q2的电量一定大于Q1的电量 | |
| C. | b点的电场强度最大 | |
| D. | 粒子由a点运动到c点运动过程中,粒子的电势能先增大后减小 |
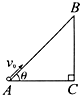 如图所示:长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q、质量为m的小球以初速度v0从斜面底端A点开始沿斜面上滑,当到达斜面顶端B点时,速度仍为v0,则( )
如图所示:长为L、倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q、质量为m的小球以初速度v0从斜面底端A点开始沿斜面上滑,当到达斜面顶端B点时,速度仍为v0,则( )| A. | 小球在B点的电势能一定大于在A点的电势能 | |
| B. | A、B两点间的电压一定等于$\frac{mgLsinθ}{q}$ | |
| C. | 若电场是匀强电场,则该电场的电场强度最大值一定为$\frac{mg}{q}$ | |
| D. | 若该电场是由放置在C点的点电荷Q产生,则θ为45° |
 如图甲所示,M、N是真空中两个电荷量均为+Q的固定点电荷,M、N间的距离为a;沿MN连线的中垂线建立坐标轴,P是x轴上的点,∠OPM=30°.已知静电力常量为k
如图甲所示,M、N是真空中两个电荷量均为+Q的固定点电荷,M、N间的距离为a;沿MN连线的中垂线建立坐标轴,P是x轴上的点,∠OPM=30°.已知静电力常量为k
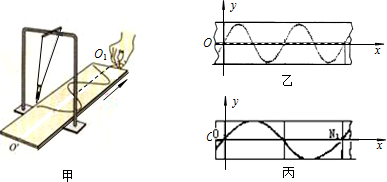
 半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一光束沿半径方向与OO′成θ=30°射向O点,光屏PQ区域出现两个光斑.当θ逐渐增大到45°时,光屏上的两个光斑恰好变成一个.试求:
半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′为直径MN的垂线.足够大的光屏PQ紧靠在玻璃砖的右侧且与MN垂直.一光束沿半径方向与OO′成θ=30°射向O点,光屏PQ区域出现两个光斑.当θ逐渐增大到45°时,光屏上的两个光斑恰好变成一个.试求: