题目内容
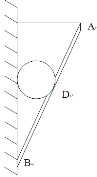
【题目】如图所示,一轻杆AB把一重力为G的光滑球夹在墙的中间,杆与墙的夹角θ=300,杆的B端用绞链固定在墙上,杆的A端用绳子水平拉住,D点为球与杆的接触点,D为杆AB的中点,求墙对杆B端的作用力。
【答案】方向:与墙夹角300左斜向上,大小:F=G/cos300
【解析】
试题分析:对球进行受力分析,
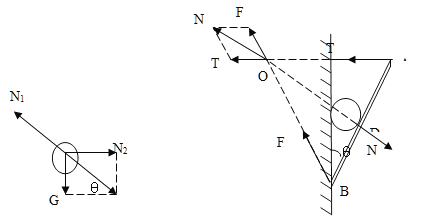
N1=G/sin300=2G
对杆进行受力分析,由于是轻杆,没有重力,杆受绳子的拉力T,球对杆的压力N1,此二力的力的作用线交于O点,据三力汇交原理得:墙对杆B点的作用力也要过O点,如图所示,所以墙对杆B点作用力的方向为与墙夹角300左斜向上。据几何知识,ΔOAB为等边三角形,则∠FOT=600
平行四边形OTN1F为菱形,则有: N1=2Fcos300=2G
解得:F=G/cos300

练习册系列答案
相关题目
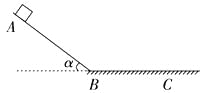
【题目】如图所示,t=0时,质量为0.5 kg的物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(经过B点前后速度大小不变),最后停在C点。每隔2 s物体的瞬时速度记录在下表中,重力加速度g=10 m/s2,则下列说法中正确的是( )
t/s | 0 | 2 | 4 | 6 |
v (m·s-1) | 0 | 8 | 12 | 8 |
A. t=3 s的时刻物体恰好经过B点
B. t=8 s的时刻物体恰好停在C点
C. 物体运动过程中的最大速度为12 m/s
D. A、B间的距离小于B、C间的距离