题目内容
竖直平面内有一形状为抛物线的光滑曲面轨道，如图所示，抛物线方程是y＝x2，轨道下半部分处在一个水平向外的匀强磁场中，磁场的上边界是y＝a的直线(图中虚线所示)，一个小金属环从抛物线上y＝b(b>a)处以速度v沿抛物线下滑，假设抛物线足够长，金属环沿抛物线下滑后产生的焦耳热总量是( )
A．mgb B.mv2
C．mg(b－a) D．mg(b－a)＋mv2
【答案】
D.
【解析】小金属环进入或离开磁场时，磁通量会发生变化，并产生感应电流，产生焦耳热；当小金属环全部进入磁场后，不产生感应电流，小金属环最终在磁场中做往复运动，由能量守恒可得产生的焦耳热等于减少的机械能，即Q＝mv2＋mgb－mga＝mg(b－a)＋mv2.
练习册系列答案
阅读快车系列答案
相关题目
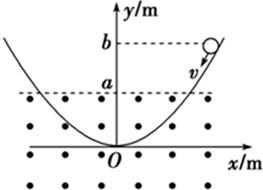
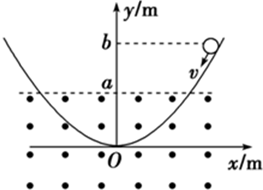竖直平面内有一形状为抛物线的光滑曲面轨道，如图所示，抛物线方程是y=x2，轨道下半部分处在一个水平向外的匀强磁场中，磁场的上边界是y=a的直线（图中虚线所示），一个小金属环从抛物线上y=b（b＞a）处以速度v沿抛物线下滑，假设抛物线足够长，金属环沿抛物线下滑后产生的焦耳热总量是（ ）
C.mg(b－a) D.
mv2
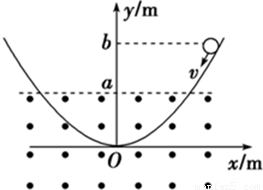
mv2